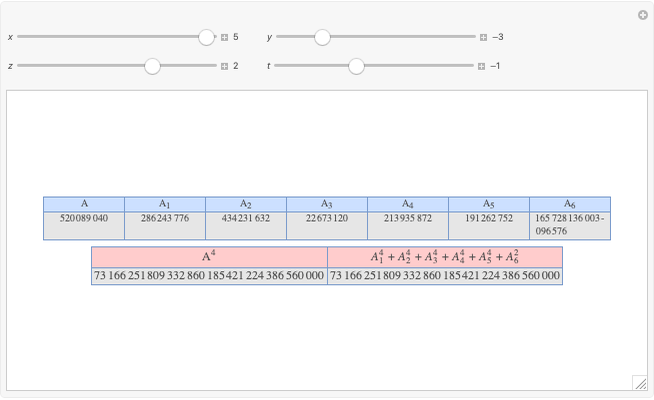
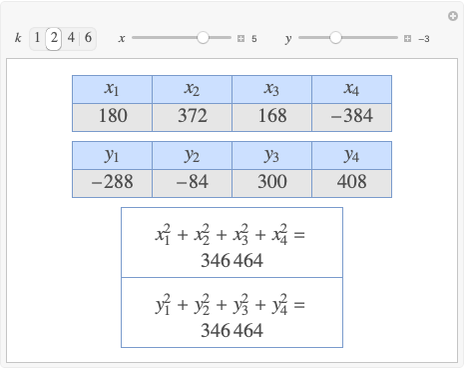
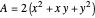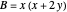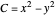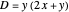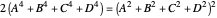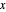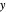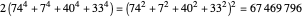A Four-Term Algebraic Identity with Squares and Quartics
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
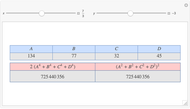
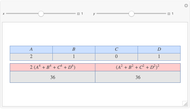
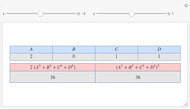
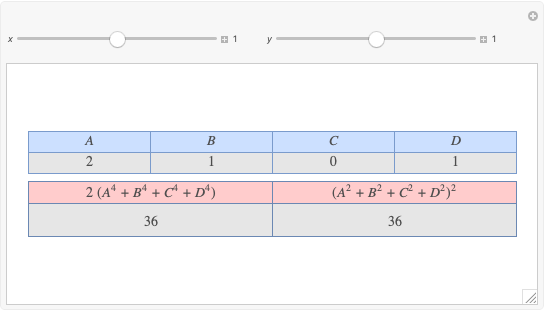
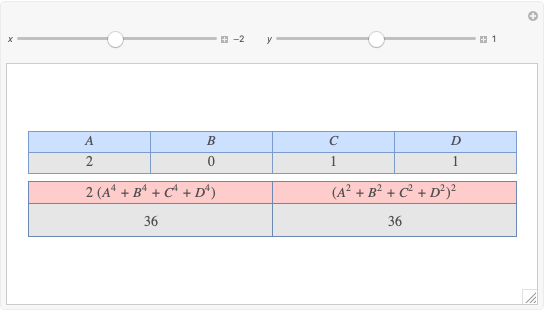
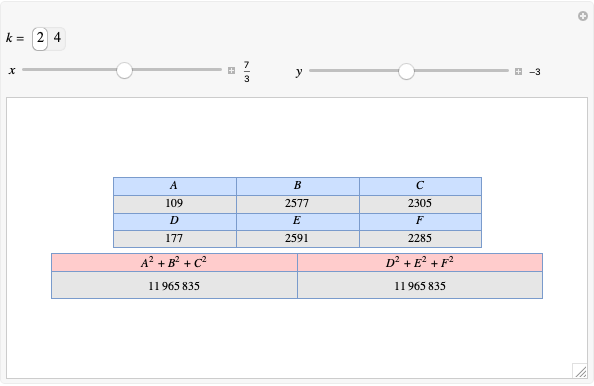
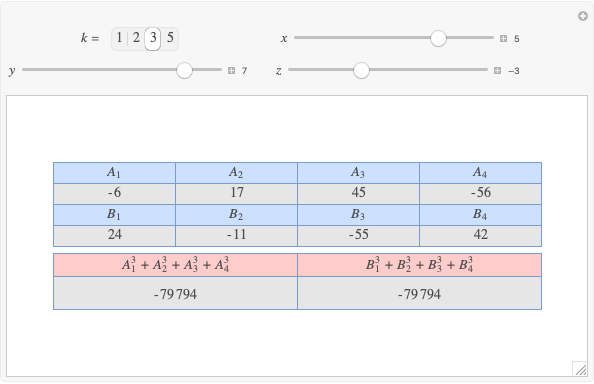
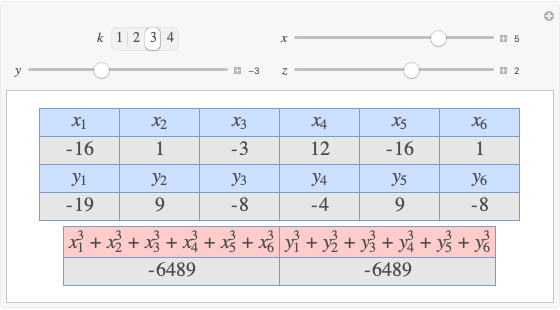
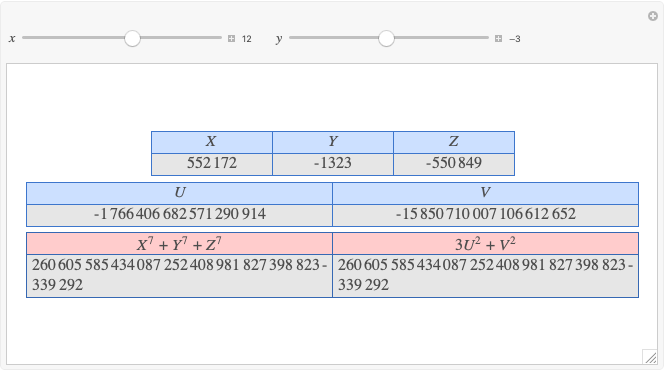
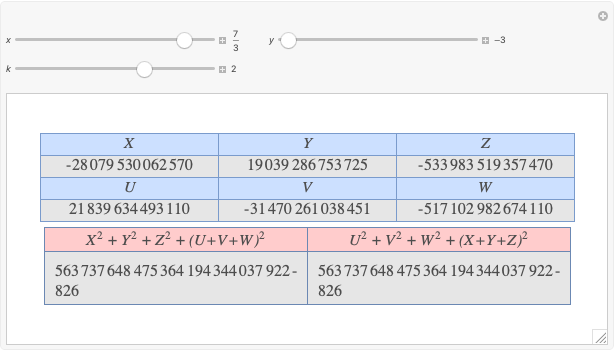
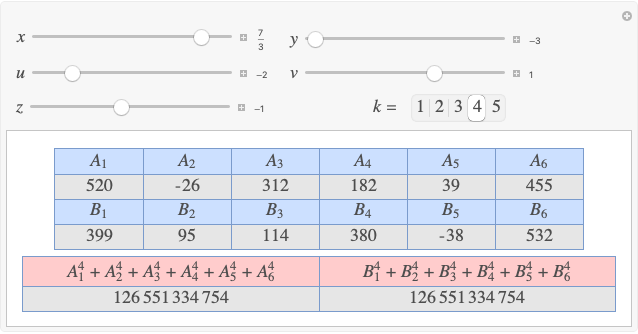
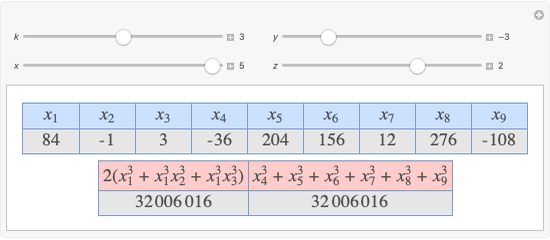
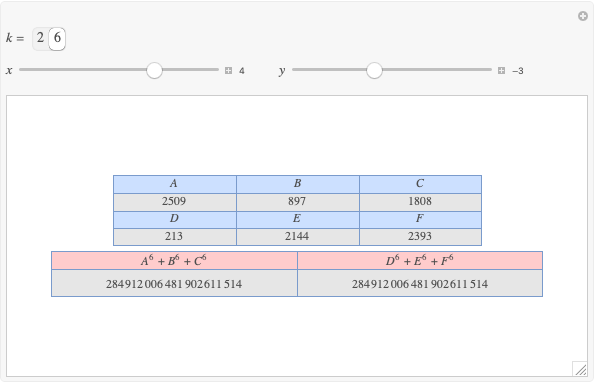
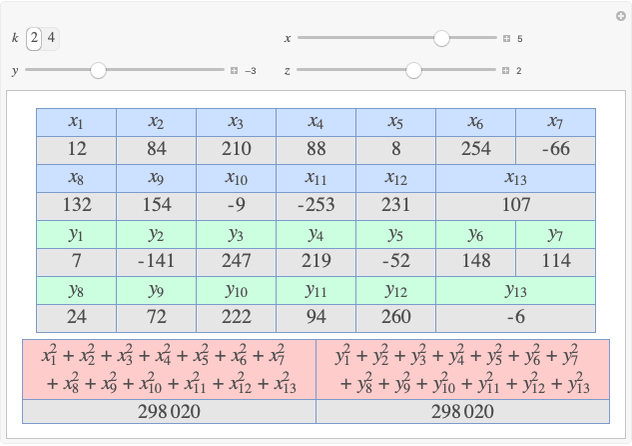
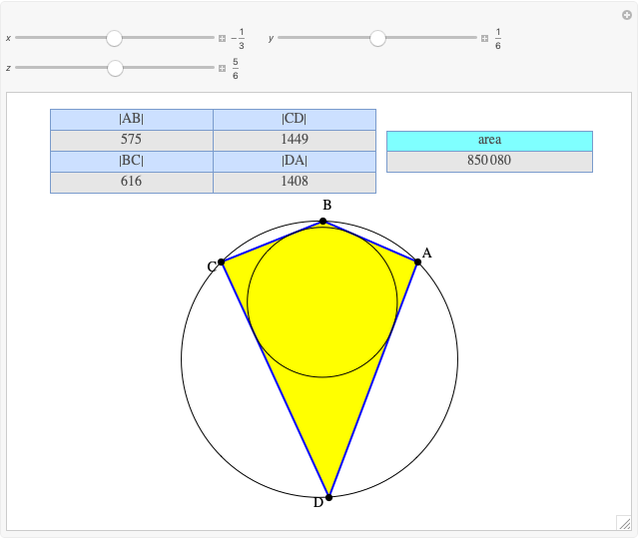
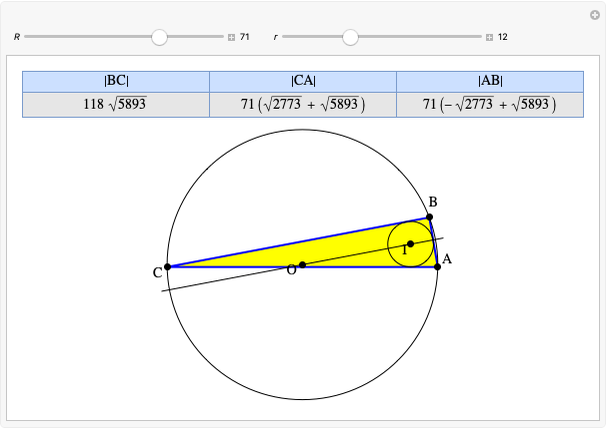
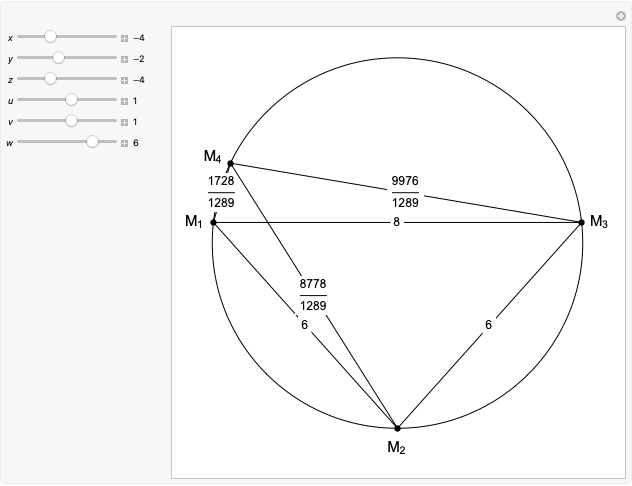
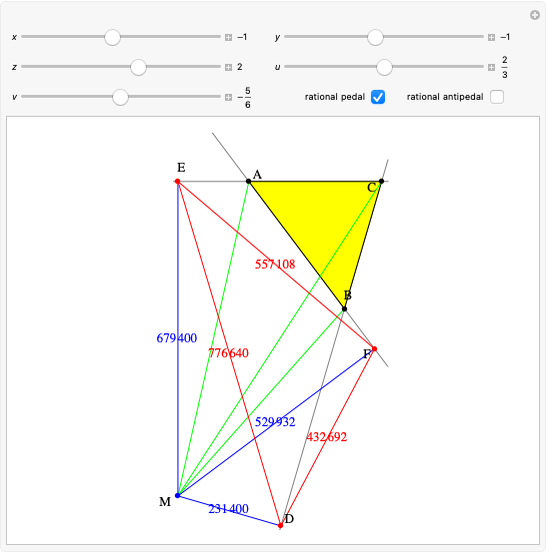
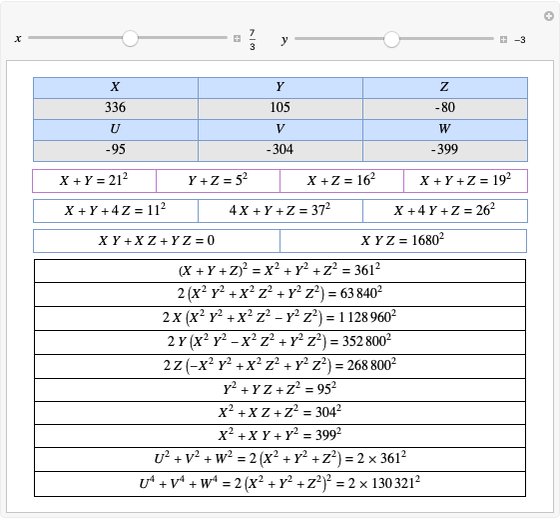
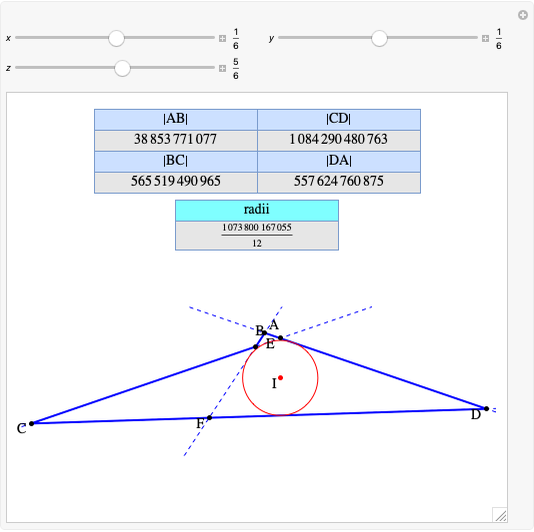
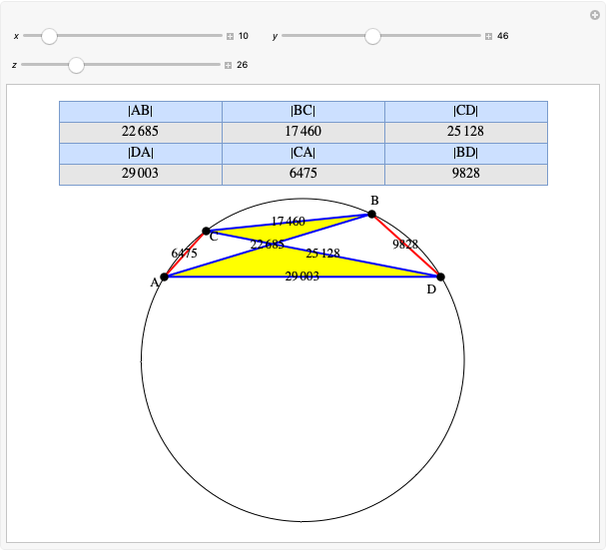
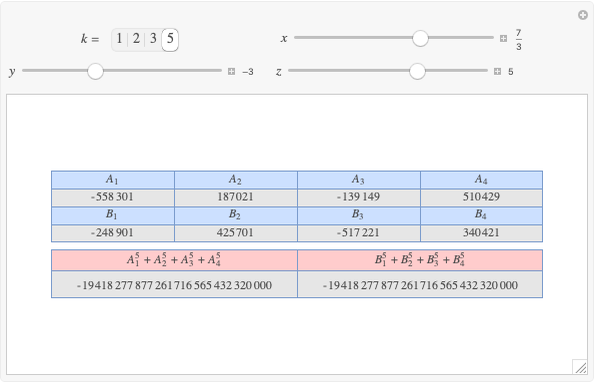
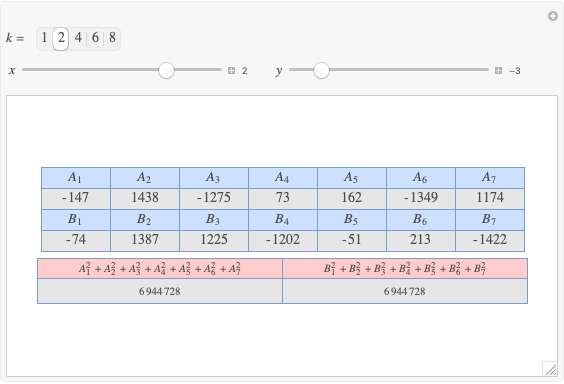
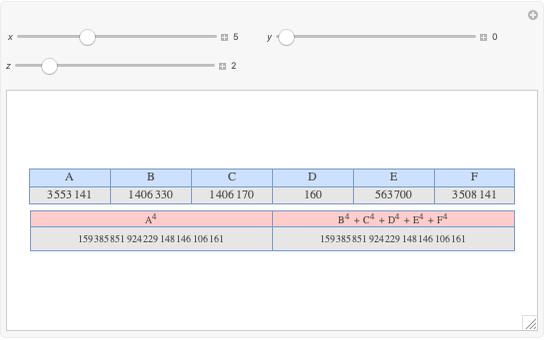
Let 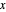 ,
, 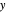 be two arbitrary numbers.
be two arbitrary numbers.
Contributed by: Minh Trinh Xuan (June 14)
Open content licensed under CC BY-NC-SA
Details
Snapshots
Permanent Citation