Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

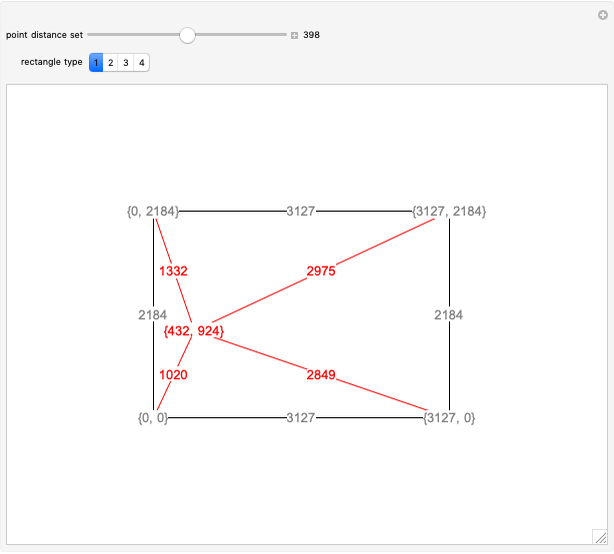
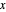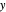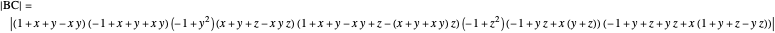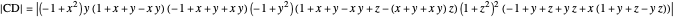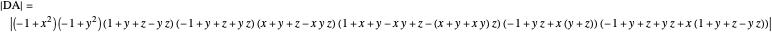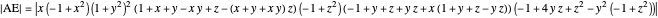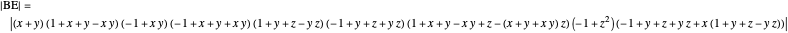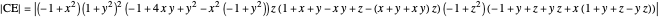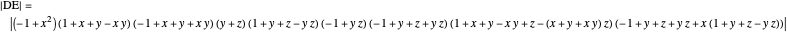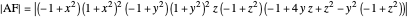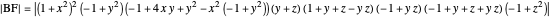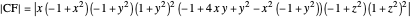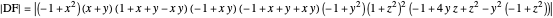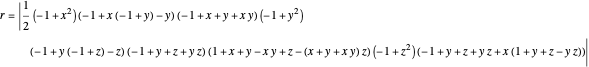Rational Tangential Complete Quadrilateral

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

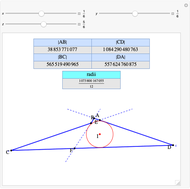
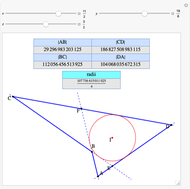
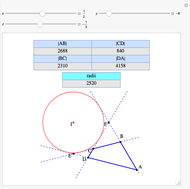
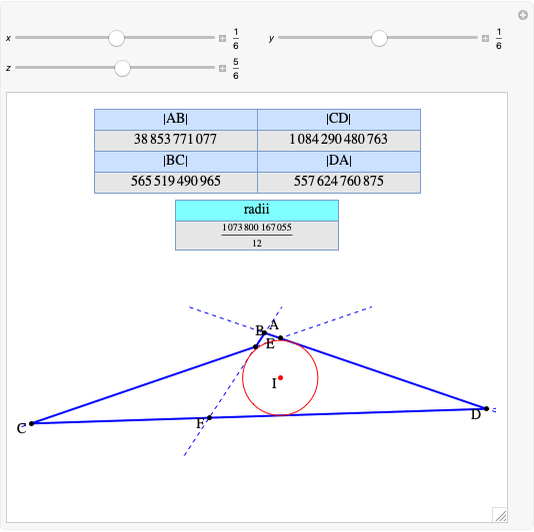
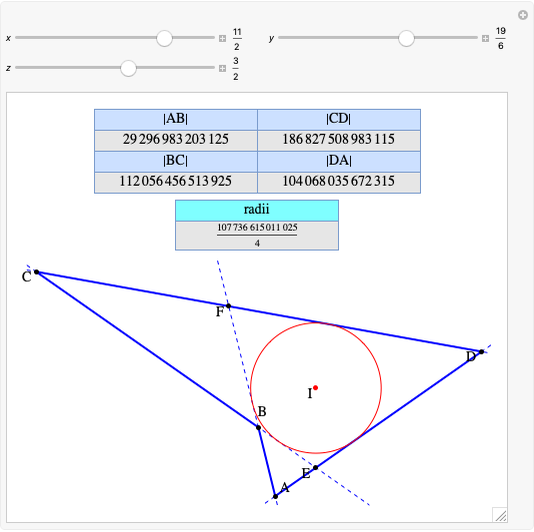
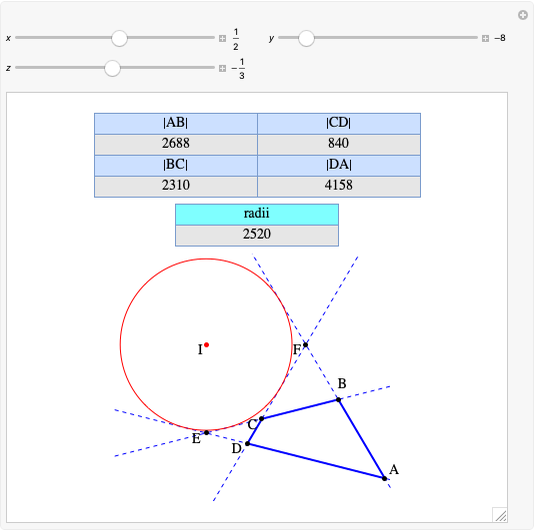
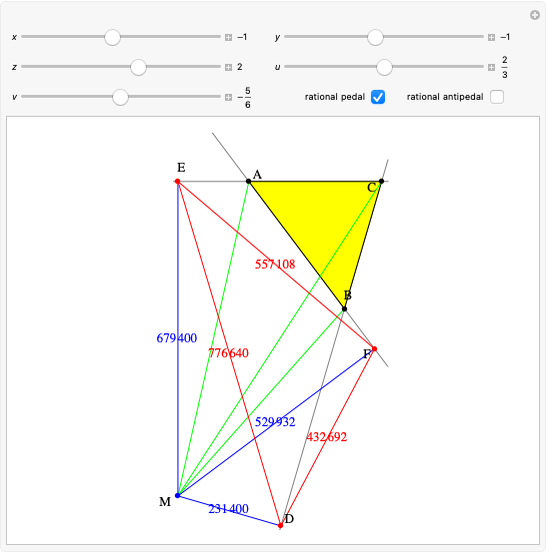
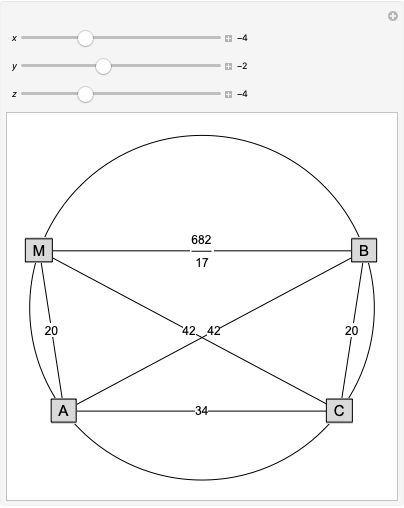
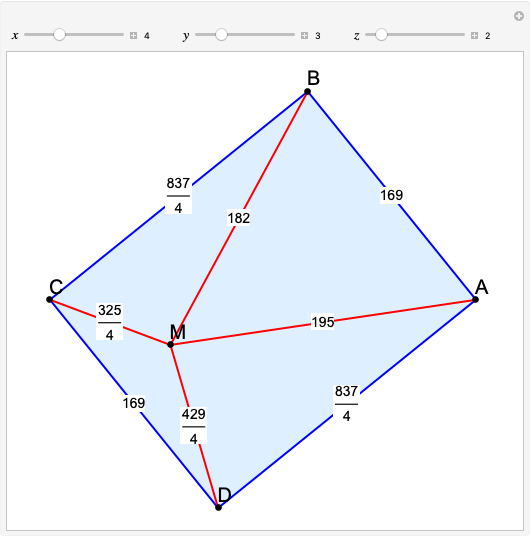
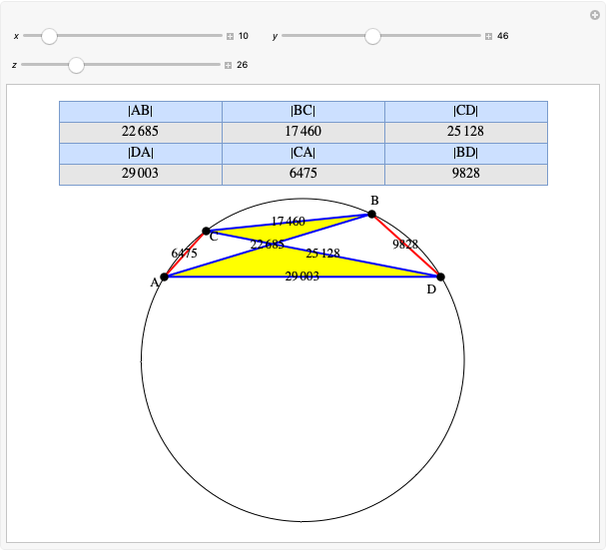
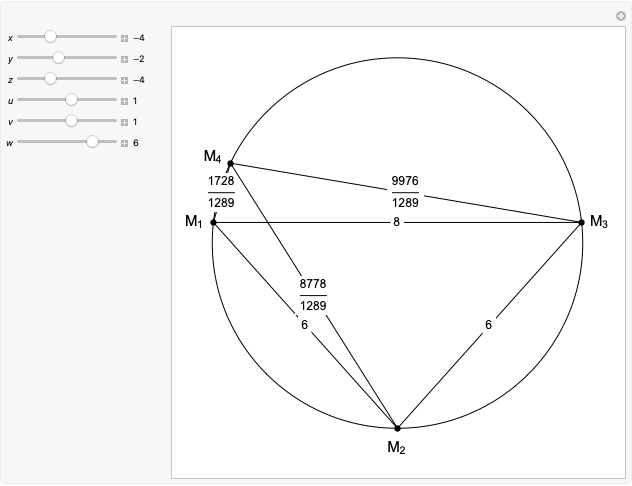
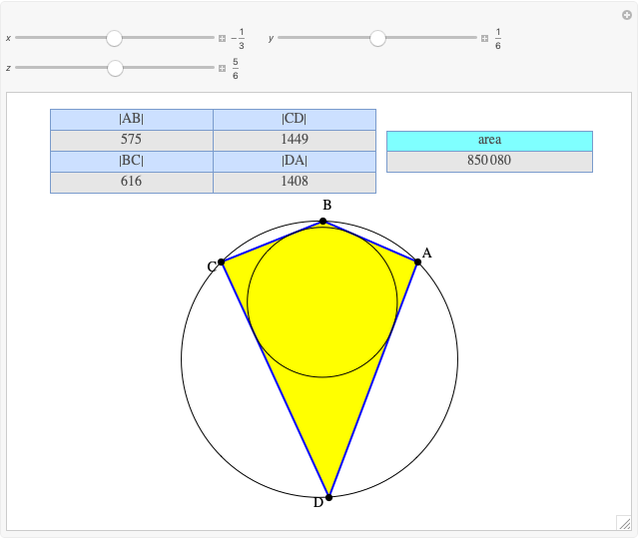
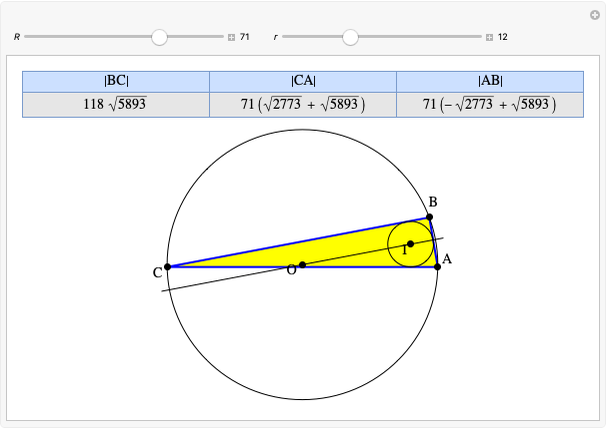
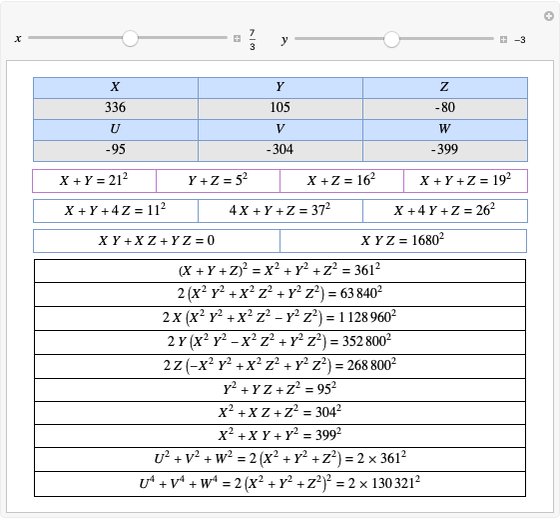
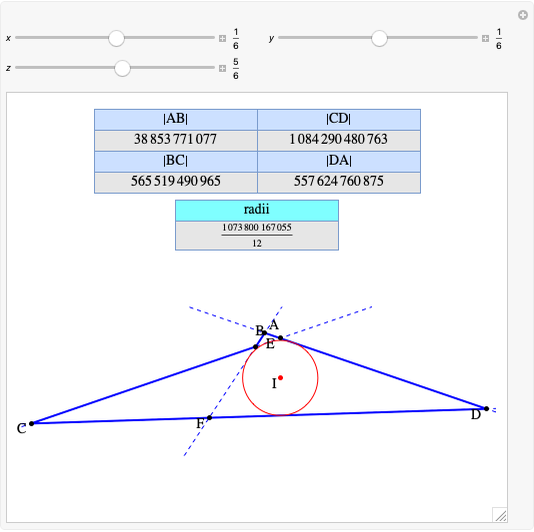
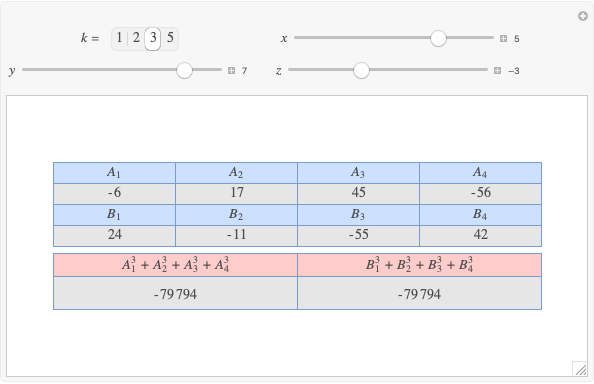
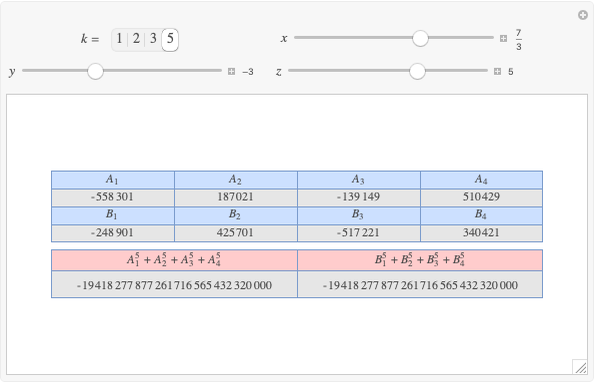
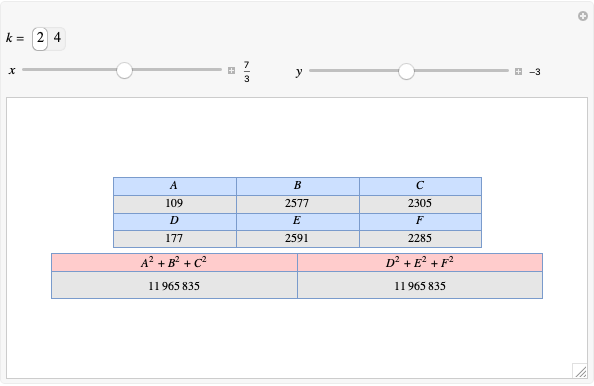
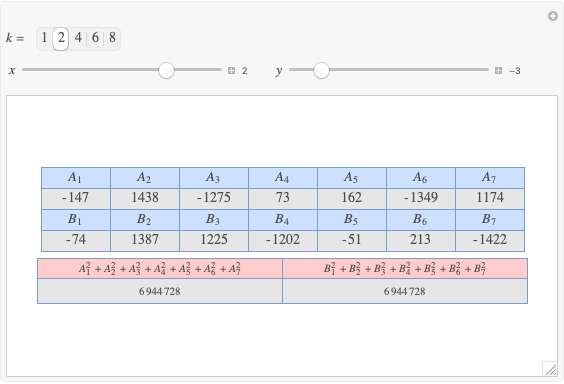
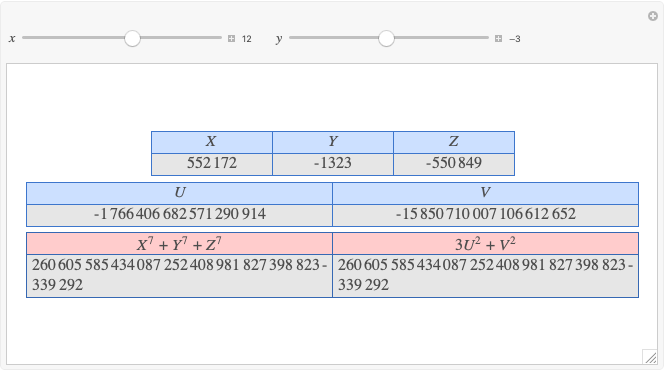
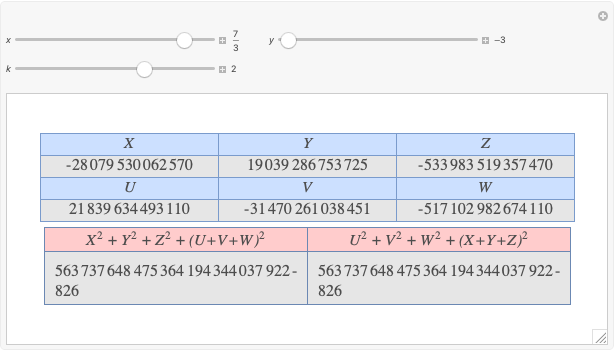
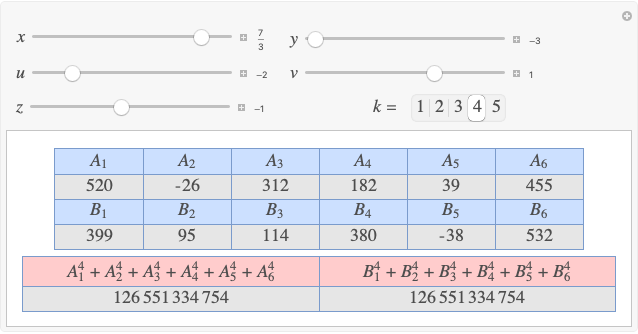
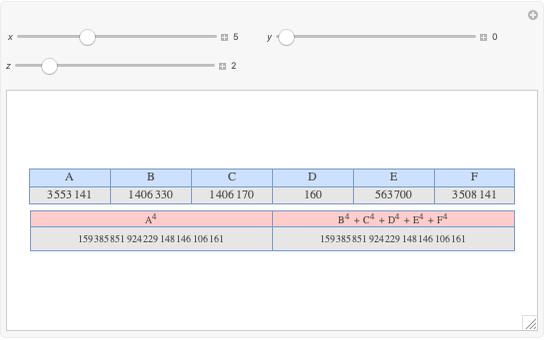
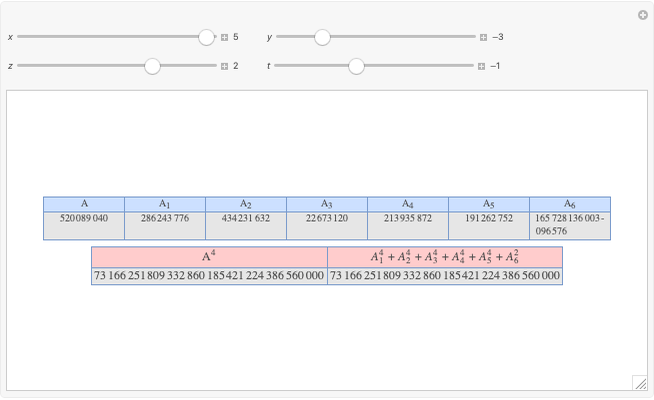
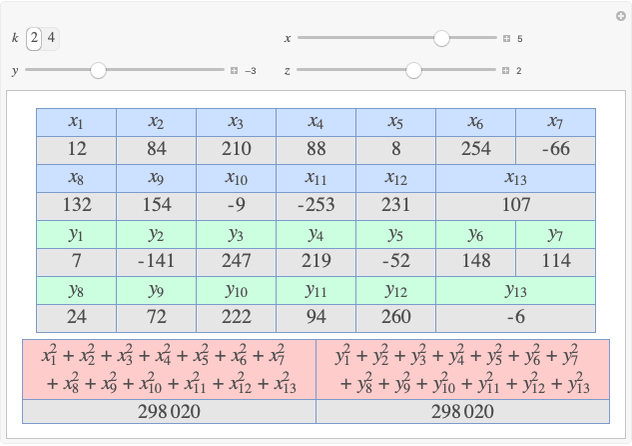
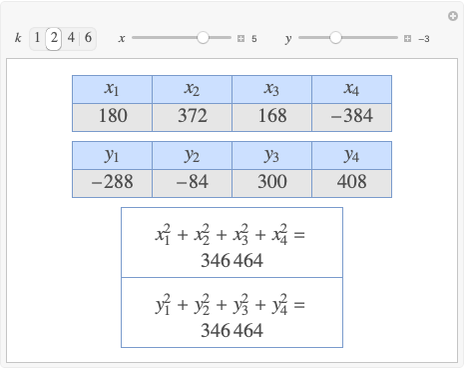
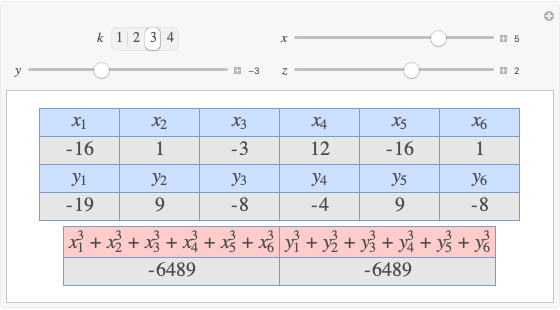
A complete quadrilateral 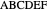is a figure with four infinite lines 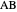, , 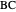, 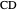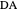with six points of intersection 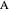, , 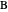, 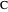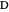and 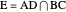, , 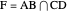where each line goes through three of the six points. Including the points 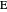and 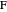, the four lines are 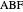, , 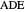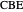and 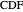. The diagonals of this quadrilateral are thus 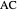, 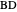and .

[more]

A tangential complete quadrilateral has all lines tangent to a circle.

A rational version has a rational distance between any two of the six points on the same line. Also, the circle has rational radius.

If , , are rational numbers, then the edge lengths of a rational tangential complete quadrilateral can be written in the following form:

,

,

,

,

,

,

,

,

,

,

,

,

.

[less]

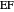Contributed by: Minh Trinh Xuan (June 13)
Open content licensed under CC BY-NC-SA

Details

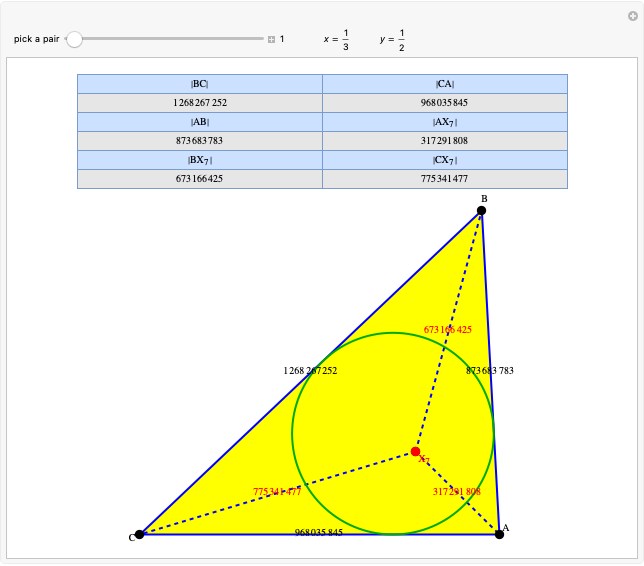
Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send