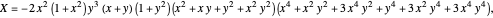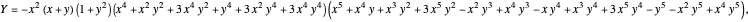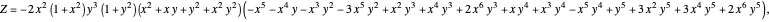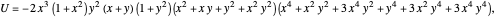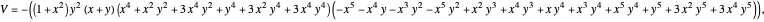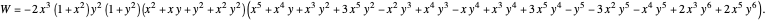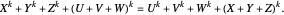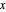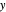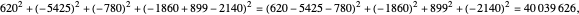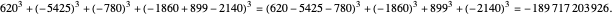Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

A Six-Variable Algebraic Identity with Squares and Cubes

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

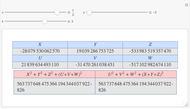
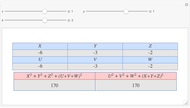
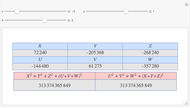
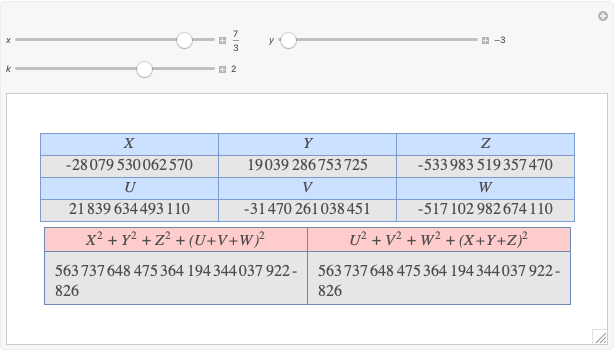
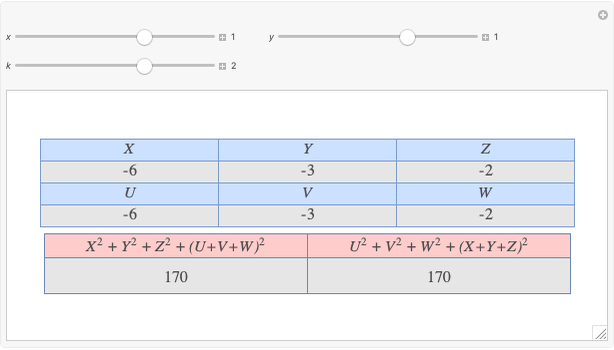
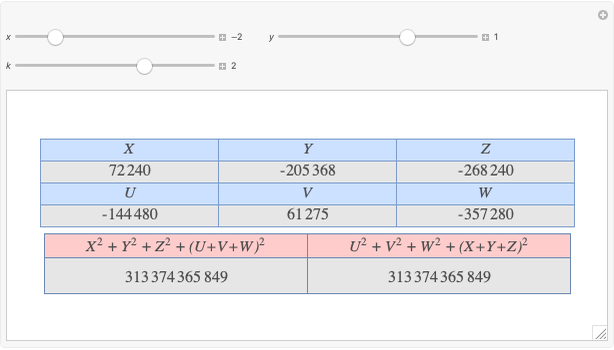
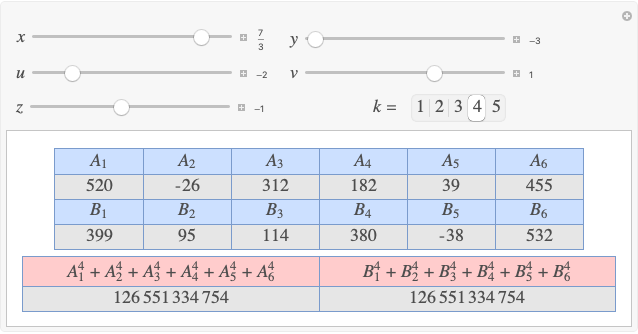
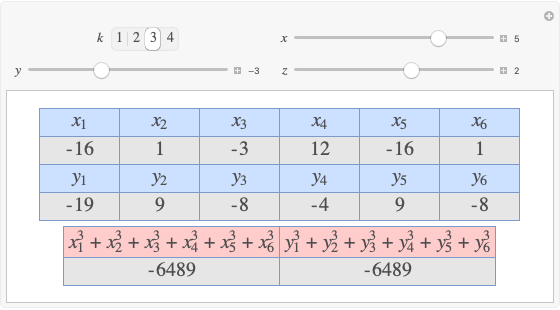
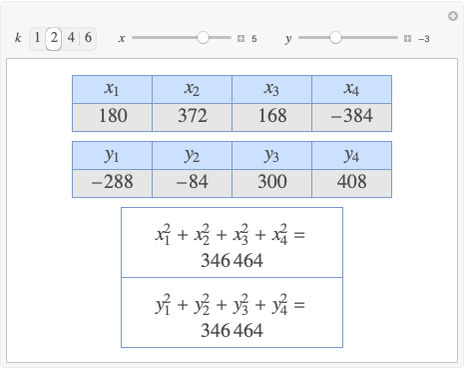
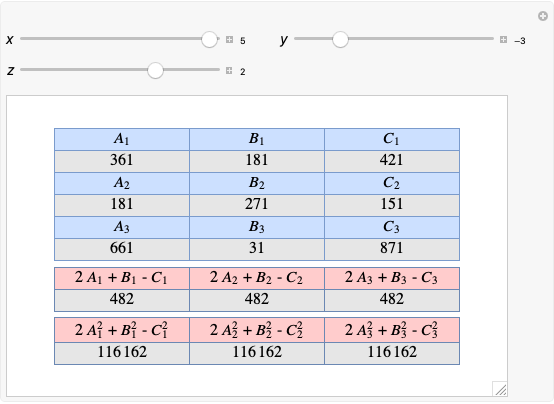
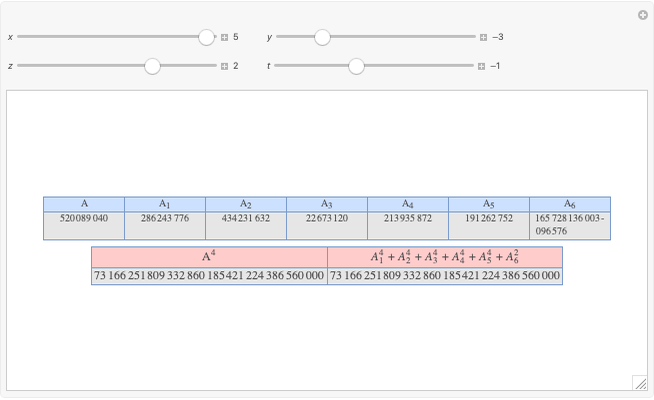
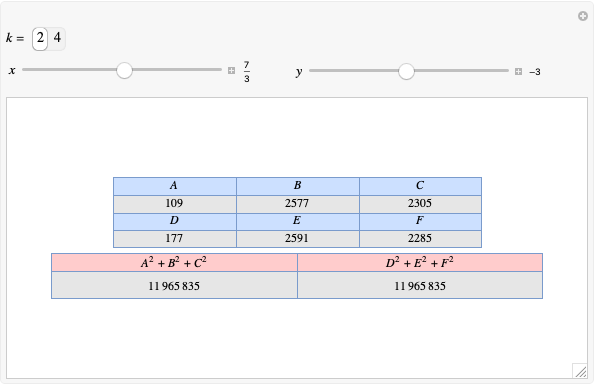
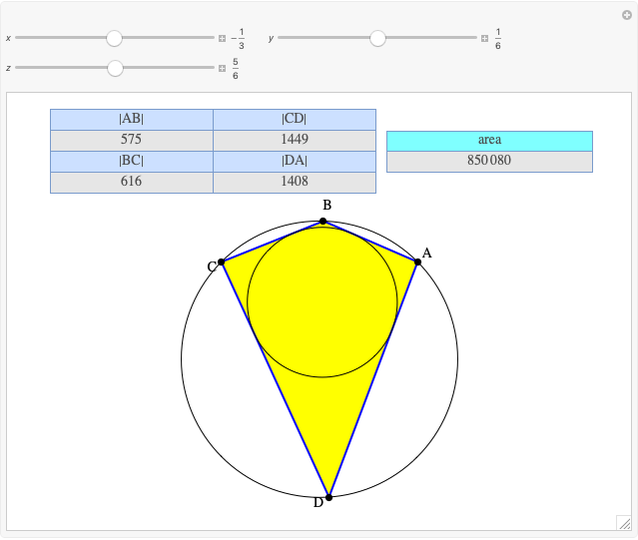
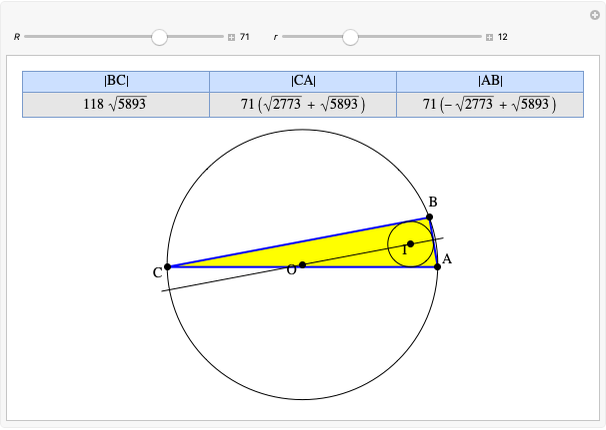
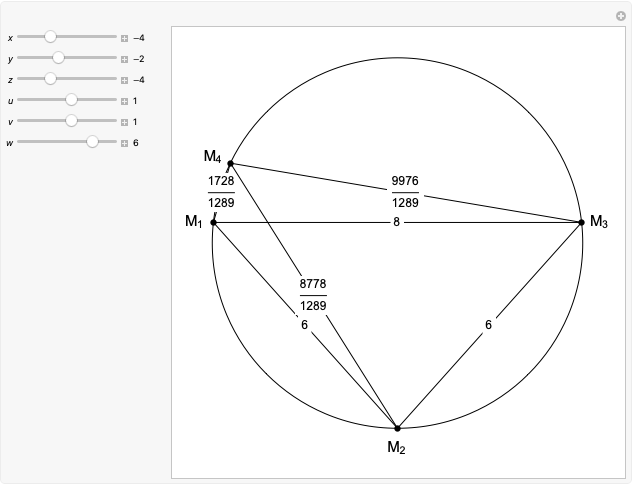
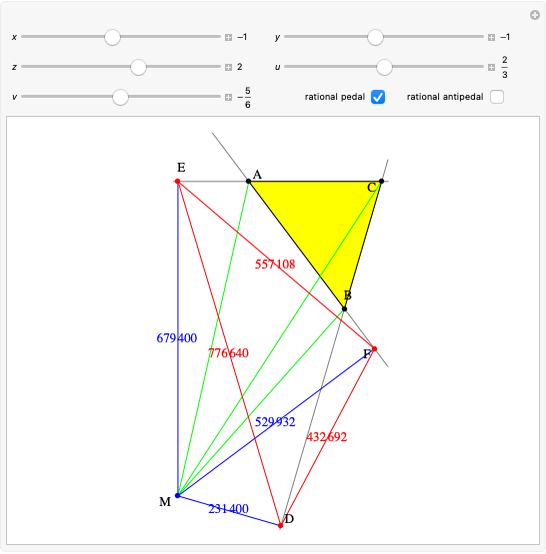
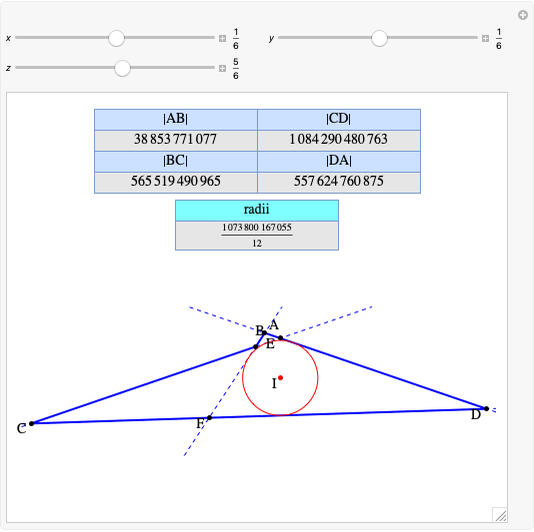
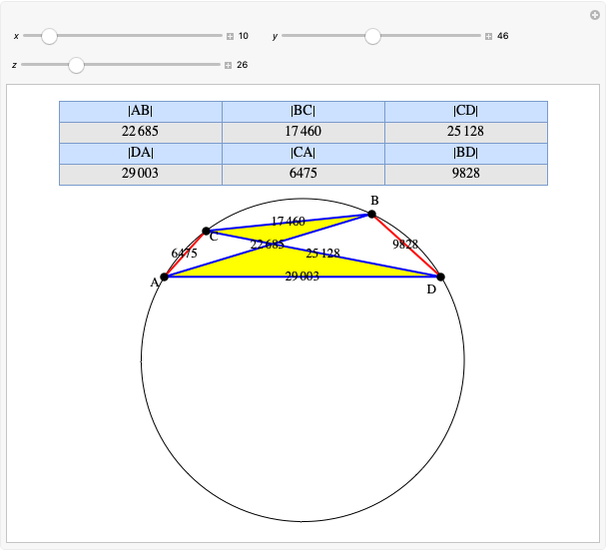
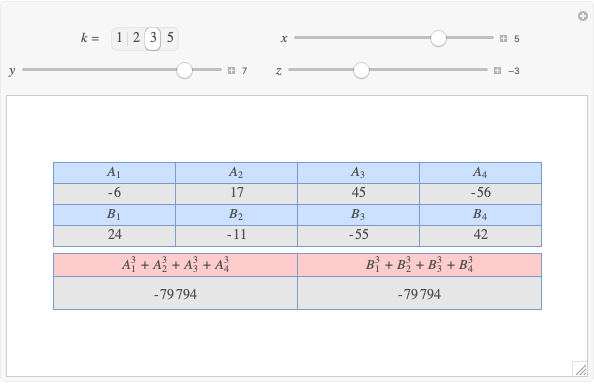
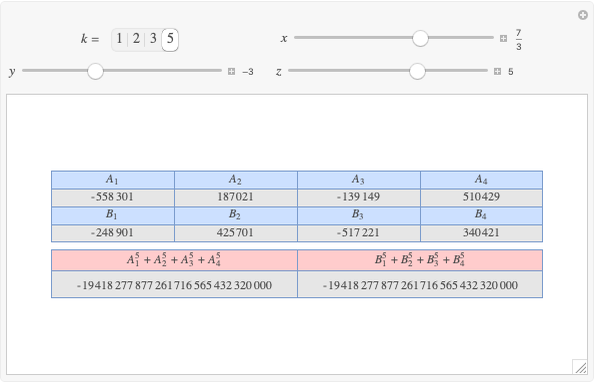
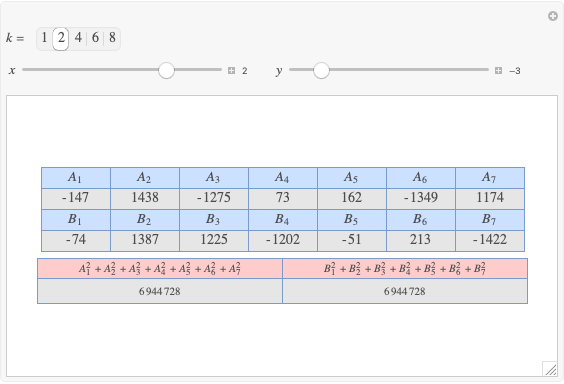
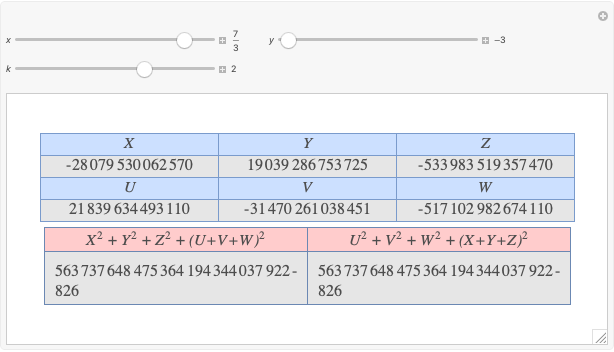
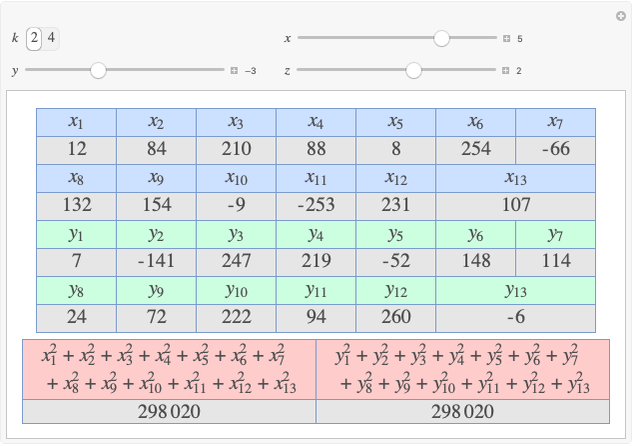
Given three rational numbers , 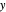and , define the following six quantities:

[more]

Then for we have

In this Demonstration, and are integers.

For example:

[less]

Contributed by: Minh Trinh Xuan (June 14)
Open content licensed under CC BY-NC-SA

Details

Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send