Age Distributions from a Leslie Model for Age-Structured Populations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
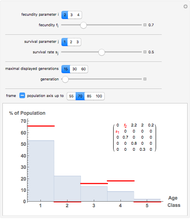
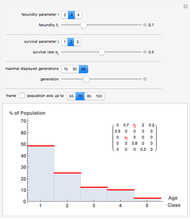
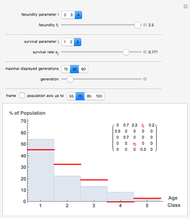
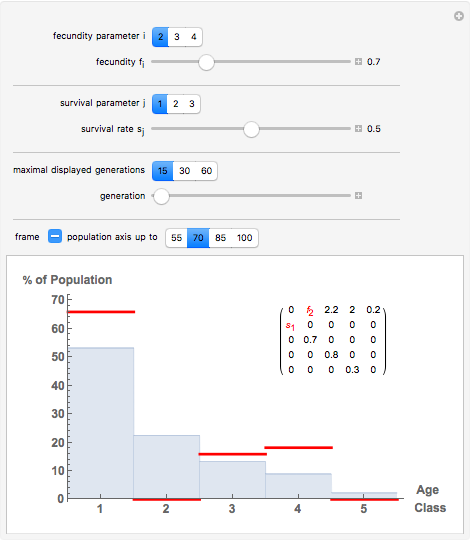
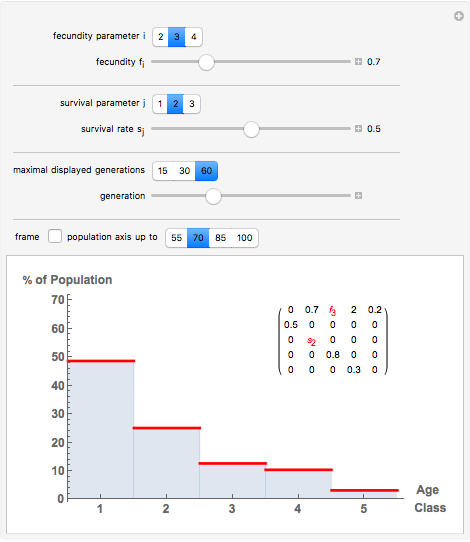
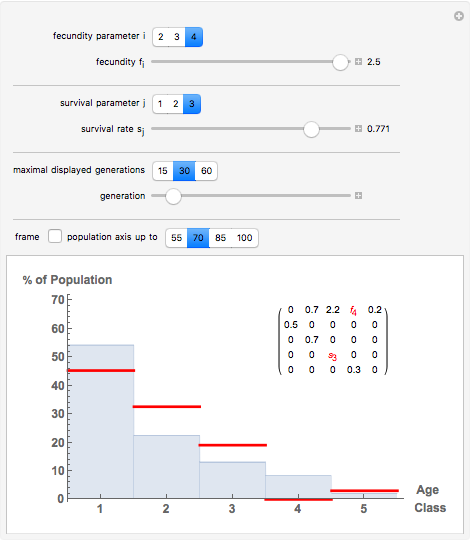
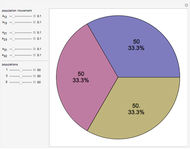
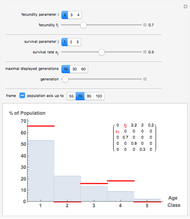
Displayed are age distributions predicted by an age-structured model based on the shown Leslie matrix 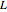 . The time evolution of the distributions (marked in red) can be followed by changing the generation slider up to the maximal chosen value. The infinite time limit is indicated by the blue distribution with filling.
. The time evolution of the distributions (marked in red) can be followed by changing the generation slider up to the maximal chosen value. The infinite time limit is indicated by the blue distribution with filling.
Contributed by: J. Ackermann and H. Hogreve (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In age-structured models of populations, age classes or "cohorts" are introduced to distinguish individuals at different life stages. For  , where
, where  is the number of different age classes, let
is the number of different age classes, let 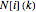 denote the number of individuals that are in cohort
denote the number of individuals that are in cohort 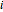 at the discrete time (generation)
at the discrete time (generation) 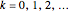 and assume an initial age distribution at
and assume an initial age distribution at  , here chosen as {0, 50%, 50%, 0, 0, 0}. In the population model put forward by P. H. Leslie ("On the Use of Matrices in Certain Population Mathematics," Biometrika, 33(3), 1945 pp. 183–212), the evolution from the given initial age distribution is determined by the recursion
, here chosen as {0, 50%, 50%, 0, 0, 0}. In the population model put forward by P. H. Leslie ("On the Use of Matrices in Certain Population Mathematics," Biometrika, 33(3), 1945 pp. 183–212), the evolution from the given initial age distribution is determined by the recursion 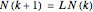 for the distribution vector
for the distribution vector 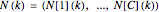 and the "Leslie matrix"
and the "Leslie matrix" 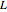 . The parameters in
. The parameters in 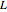 embody the survival rates yielding the fraction of the
embody the survival rates yielding the fraction of the 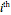 class at time
class at time  that enter into the
that enter into the 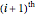 class at time
class at time  , and the "fertility" or "fecundity" coefficients giving the average number of newborns to a member of the respective cohort. The age distributions displayed are computed as
, and the "fertility" or "fecundity" coefficients giving the average number of newborns to a member of the respective cohort. The age distributions displayed are computed as 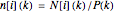 , where
, where 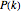 is the total population size at time
is the total population size at time  . It can be shown (by invoking the Perron–Frobenius theorem) that if
. It can be shown (by invoking the Perron–Frobenius theorem) that if 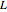 is regular then there exists an eigenvector with strictly positive components; this eigenvector yields the ''equilibrium" age distribution to which the evolution converges upon time
is regular then there exists an eigenvector with strictly positive components; this eigenvector yields the ''equilibrium" age distribution to which the evolution converges upon time  growing to infinity.
growing to infinity.
Permanent Citation