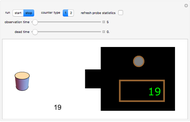
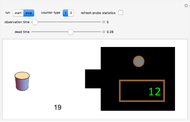
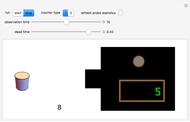
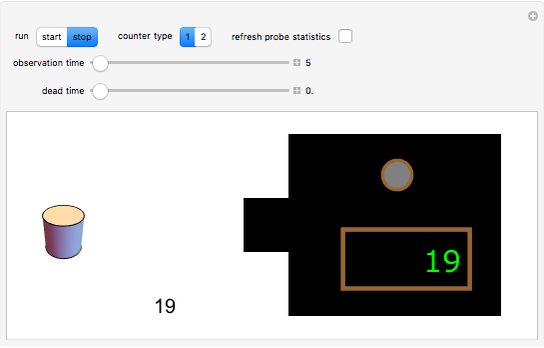
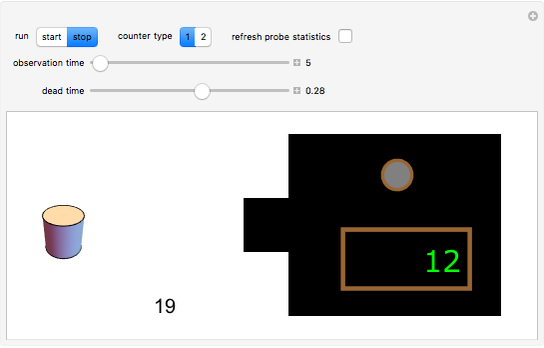
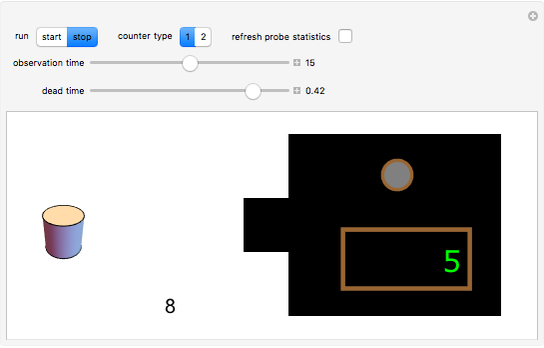
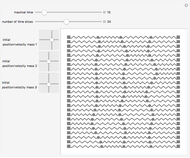
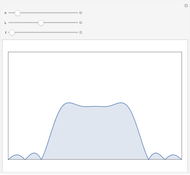
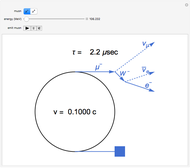
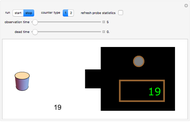
In this Demonstration, the left-hand side shows a probe of radioactive material that randomly emits beta particles in accordance with Poisson statistics, with exponentially distributed inter-event times. These events are detected by the counter displayed in the lower middle part. The Geiger counter on the right records the emitted particles. The ability of the Geiger counter to resolve subsequently arriving particles is limited by its dead time, which can be varied from 0 to some maximal value by the corresponding slider. Depending on their respective dead-time characteristics, one distinguishes between non-paralyzable ("type I") and paralyzable ("type II") counters. Type I counters get blocked and are insensitive to new events during a time period (their dead time) after each registered event. Type II counters, on the other hand, remain blocked during their dead time after each arriving particle, regardless of whether or not the event was registered. In the Demonstration, the green light indicates that the Geiger counter is ready for registering particles, while the red light signals that the counter is blocked. To expedite the comparison between the different counter types and values of the dead time, the random sequence of particles from the source is kept fixed; it can, however, be changed by the option "refresh probe statistics".