Approximating Volumes by Summation
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
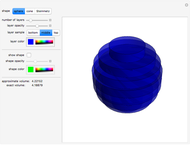
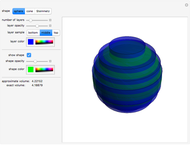
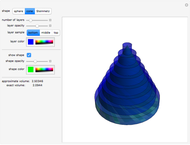
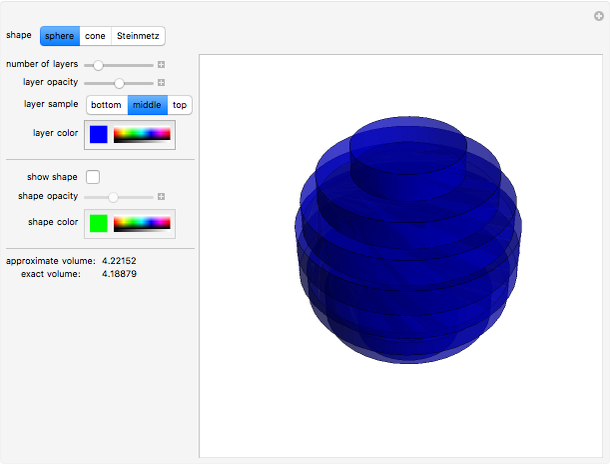
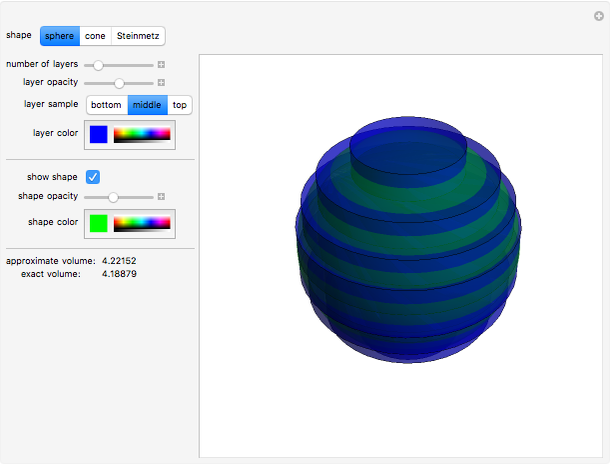
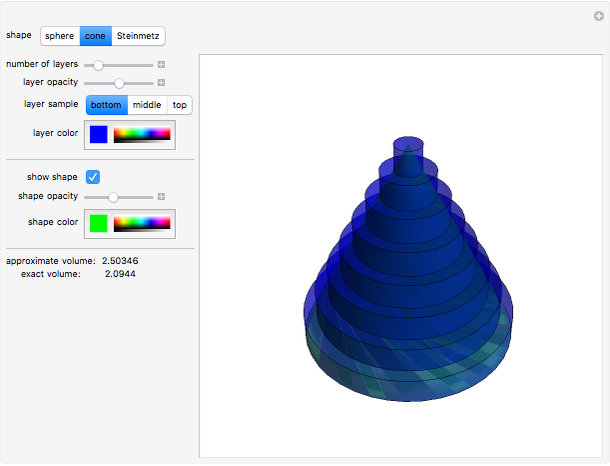
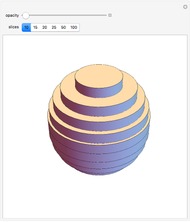
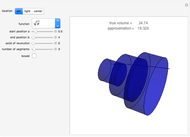
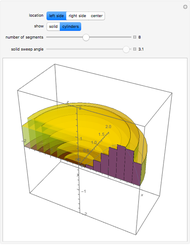
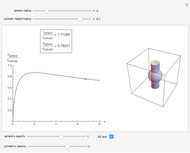
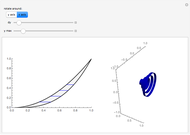
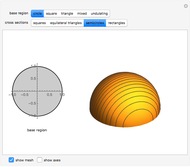
The volume of a solid shape can be approximated by slicing it into layers and summing the volumes of all of the layers. The limit of this process is an integral that yields the volume of the solid. This is an analogue of a Riemann summation of the area under a curve.
Contributed by: Jason Harris (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
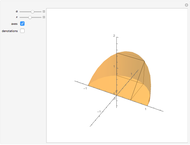
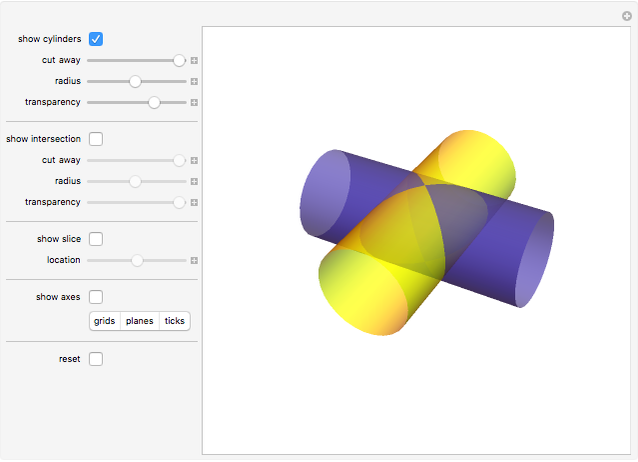
A Steinmetz solid, or a bicylinder, is the shape formed when two cylinders intersect at right angles.
Permanent Citation
"Approximating Volumes by Summation"
http://demonstrations.wolfram.com/ApproximatingVolumesBySummation/
Wolfram Demonstrations Project
Published: March 7 2011
Volume of a Cylindrical Hoof
Izidor Hafner
Approximating the Volume of a Sphere Using Cylindrical Slices
Tom De Vries
Double Integral for Volume
Anton Antonov
Volumes Using the Disc Method
Stephen Wilkerson (Towson University)
Volumes of Revolution Using Cylindrical Shells
Stephen Wilkerson (Towson University)
Intersection of Two Cylinders
Eric Schulz
Ratio of the Surface Area of a Sphere to a Cylinder
Jan Fiala
Volumes of Solids of Revolution: Shell Method
Helen Papadopoulos
Solids of Known Cross Section
Abby Brown (Torrey Pines High School)
Solids Whose Cross Sections Have the Same Shape
Glenn Beatty and Mark Evans (Science and Mathematics Academy)
