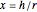Ratio of the Surface Area of a Sphere to a Cylinder

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
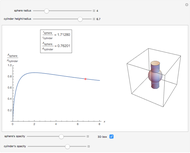
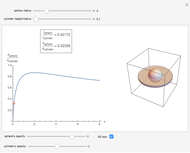
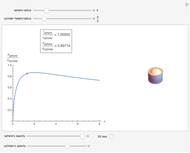
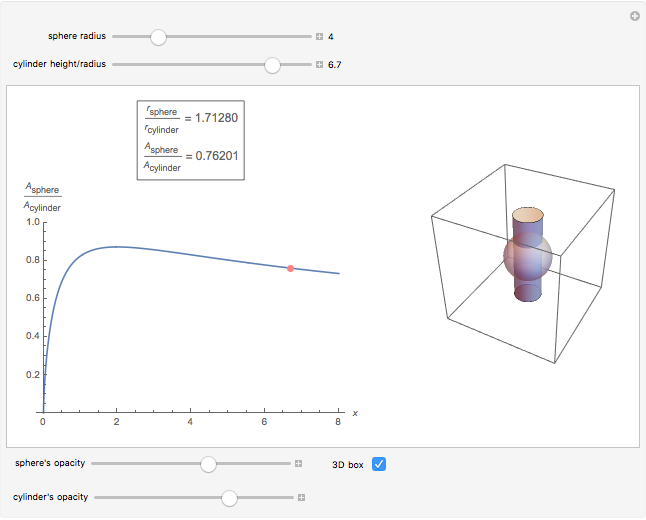
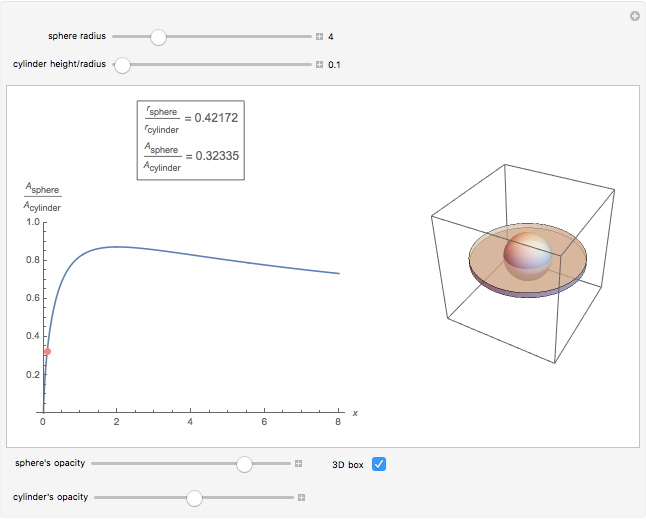
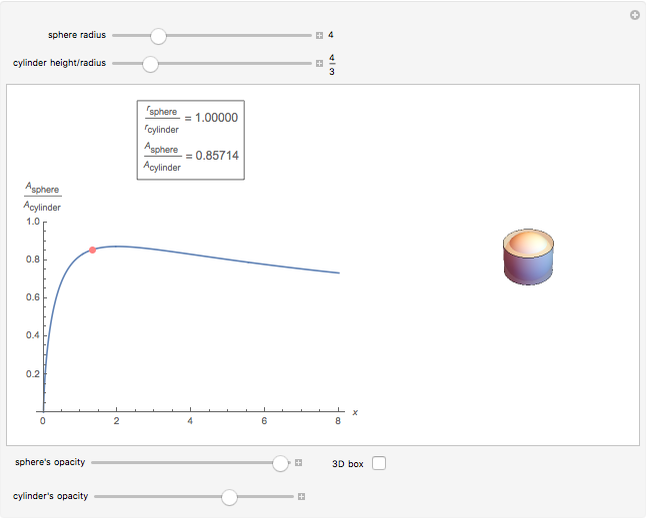
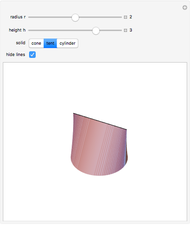
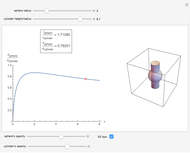
Of all the shapes, a sphere has the smallest surface area for a given volume. What about a cylinder's surface area? With a properly chosen ratio of height to radius, how close can the cylinder's surface area get to the sphere's surface area of the same volume? Use the sliders to explore these questions without calculus. The bigger the ratio  , the closer you are to a cylinder with the smallest surface for a given volume.
, the closer you are to a cylinder with the smallest surface for a given volume.
Contributed by: Jan Fiala (October 2014)
(UVa-Wise)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The control  sets the volume and scale of the plot on the right. The control
sets the volume and scale of the plot on the right. The control  determines the proportions of the cylinder (large
determines the proportions of the cylinder (large  gives a long cylinder and small
gives a long cylinder and small  gives a short cylinder). The controls at the bottom are convenient for better visualization.
gives a short cylinder). The controls at the bottom are convenient for better visualization.
Reference
[1] J. Fiala. My Edited Video [Video]. (Aug 25, 2014) www.youtube.com/watch?v=tEGWreii6dM.
Permanent Citation