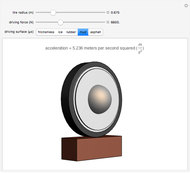
Solids Whose Cross Sections Have the Same Shape

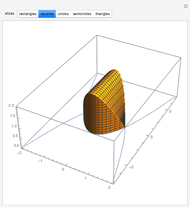
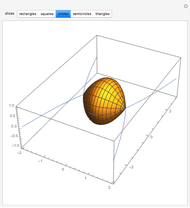
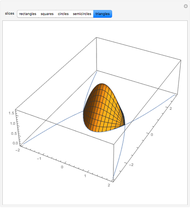
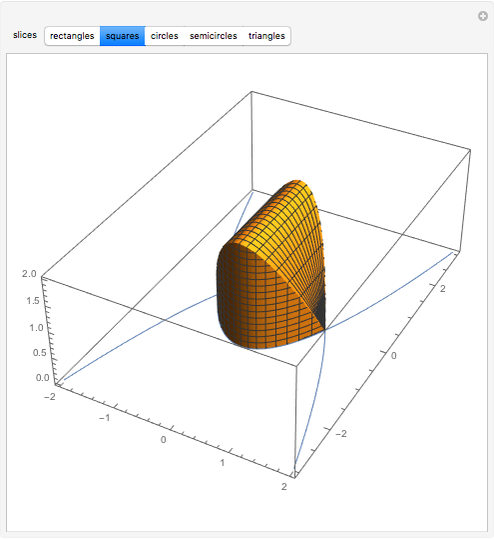
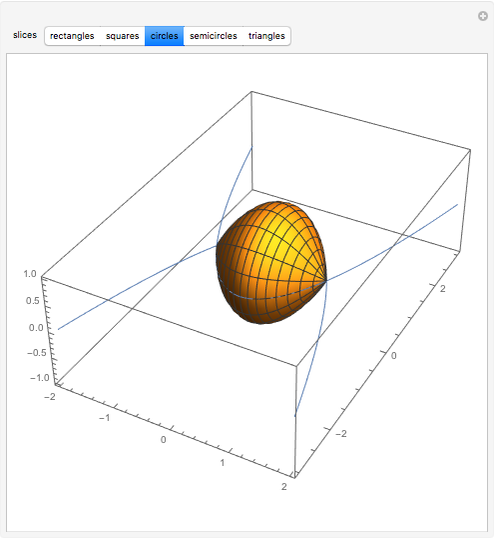
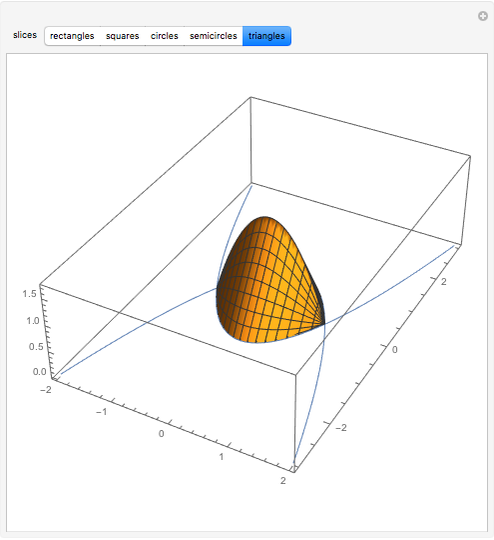
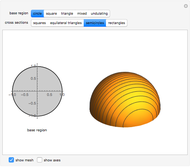
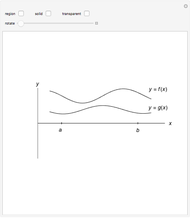
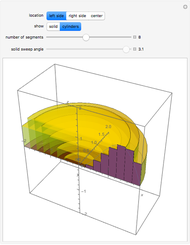
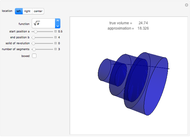
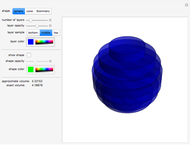
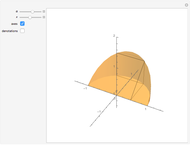
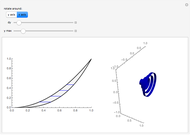
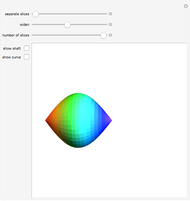
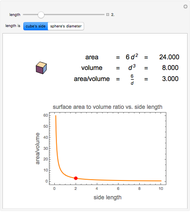
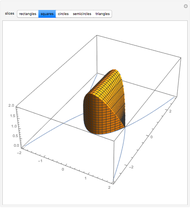
Creating areas based on the integration of heights and volumes based on the integration of areas are important concepts in calculus. Students are often asked to determine the volume of a solid, the base of which is the intersection of two curves. The cross sections of the solid perpendicular to the axis all have the same shape, with some important dimension of that shape determined by the two curves. Here are a few examples of what these solids would look like for the intersection of the curves 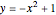, and 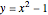. This can help students visualize the solid in question.