Asymmetric Heavy Top

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
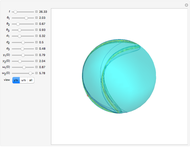
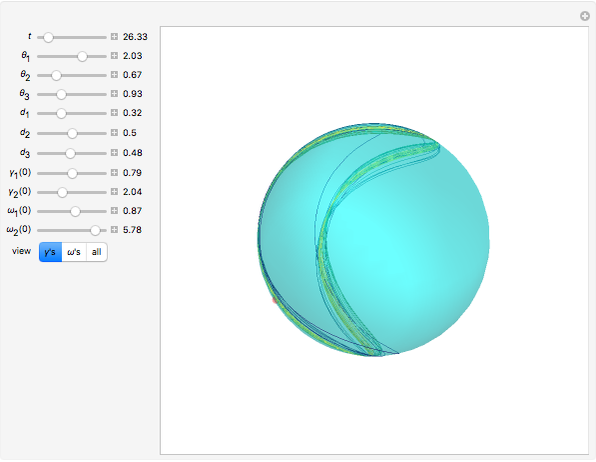
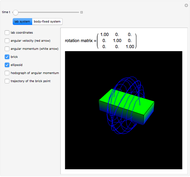
A top is a rigid body moving with one fixed point. It is classified as symmetric when the moments of inertia with respect to the  and
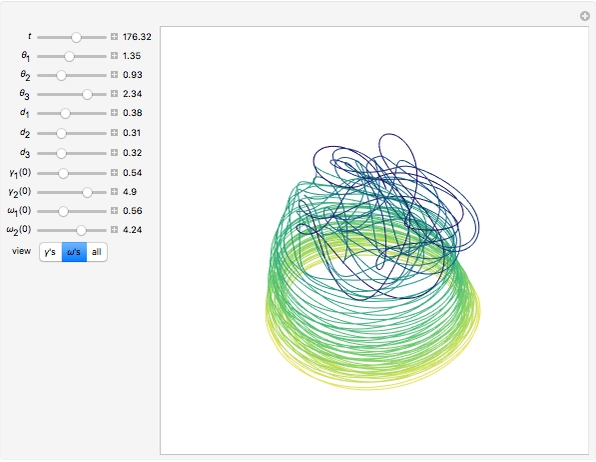
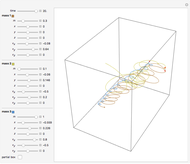
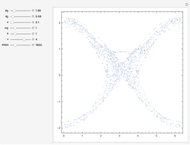
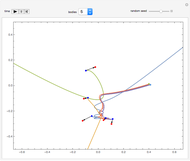
and  axes are equal, which produces periodic motion. In the case of an asymmetric top, the motion becomes chaotic. This Demonstration plots the solutions of the six first-order nonlinear differential equations describing the dynamics of an asymmetric top.
axes are equal, which produces periodic motion. In the case of an asymmetric top, the motion becomes chaotic. This Demonstration plots the solutions of the six first-order nonlinear differential equations describing the dynamics of an asymmetric top.
Contributed by: Enrique Zeleny (April 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
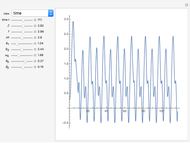
The equations for the velocity vector  (a vertical unit vector in a laboratory frame relative to the positions of the axes of the body frame) are given by
(a vertical unit vector in a laboratory frame relative to the positions of the axes of the body frame) are given by
 ,
,
 ,
,
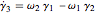 ,
,
and the Euler equations for the changes of angular momentum produced by the gravitational torque are
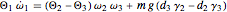 ,
,
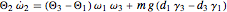 ,
,
 ,
,
where  is the angular velocity vector,
is the angular velocity vector, 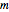 the mass of the body,
the mass of the body,  the acceleration of gravity,
the acceleration of gravity,  (a vector) represents the position of the center of gravity, and
(a vector) represents the position of the center of gravity, and 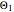 ,
,  ,
,  are the principal moments of inertia.
are the principal moments of inertia.
Reference
[1] T. Té́l and M. Gruiz, Chaotic Dynamics, An Introduction Based on Classical Mechanics, New York: Cambridge University Press, 2006.
Permanent Citation