Average Value via Integrals

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
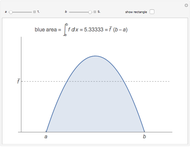
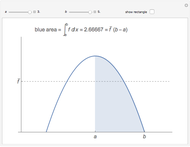
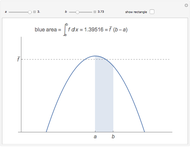
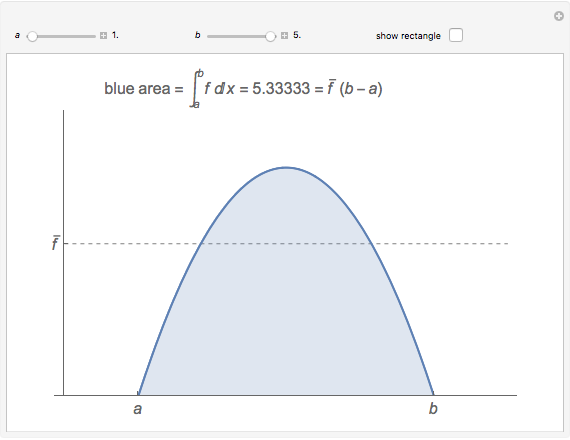
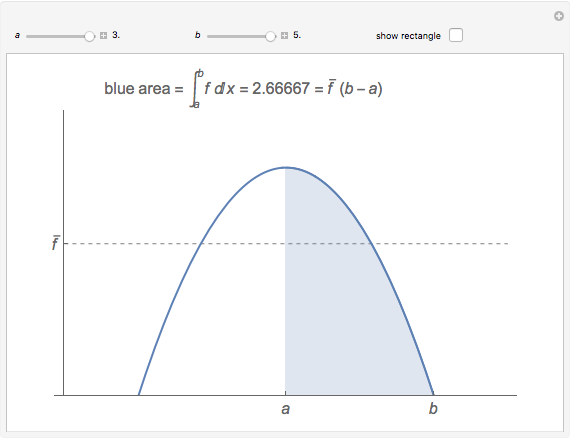
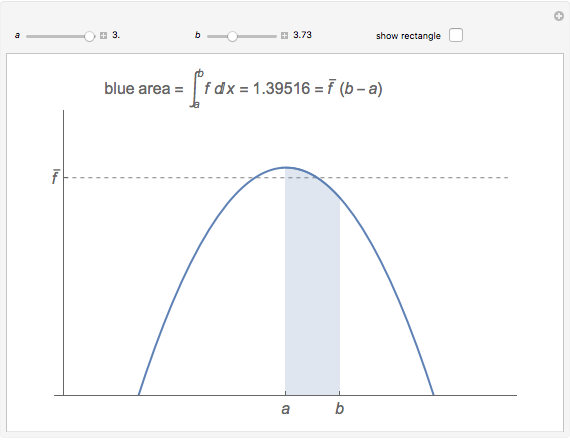
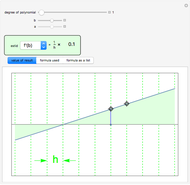
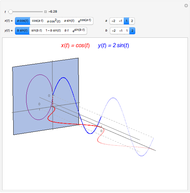
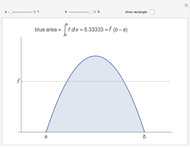
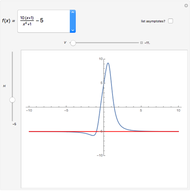
The average value of an integrable function  on an interval
on an interval  can be defined using integrals:
can be defined using integrals:  , or, equivalently,
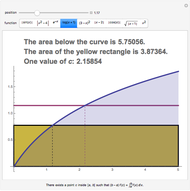
, or, equivalently,  , so, for positive functions, the average value is the height of the rectangle with width
, so, for positive functions, the average value is the height of the rectangle with width  that has the same area as the region betwen the graph
that has the same area as the region betwen the graph  and the interval
and the interval  on the
on the  axis. This Demonstration illustrates that fact.
axis. This Demonstration illustrates that fact.
Contributed by: Laura R. Lynch (May 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
When "show rectangle" is checked, notice that the blue area is the same as the red area.
Permanent Citation
"Average Value via Integrals"
http://demonstrations.wolfram.com/AverageValueViaIntegrals/
Wolfram Demonstrations Project
Published: May 20 2014