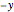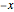Symmetry in Graphs of Functions and Relations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
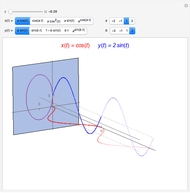
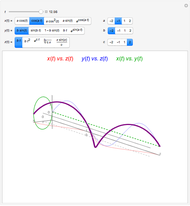
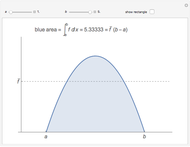
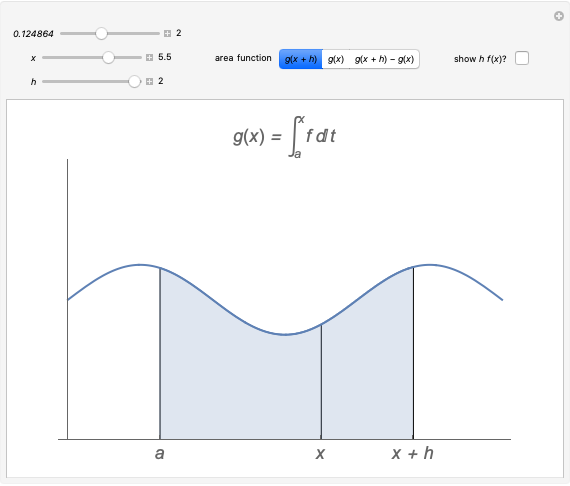
This Demonstration shows the three types of symmetry commonly studied in graphs: symmetry with respect to the  axis, the
axis, the 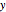 axis, or the origin.
axis, or the origin.
Contributed by: Laura R. Lynch (June 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
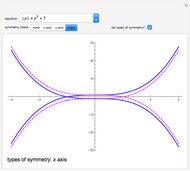
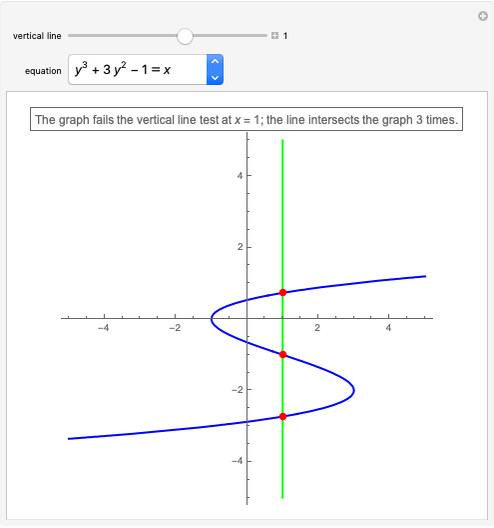
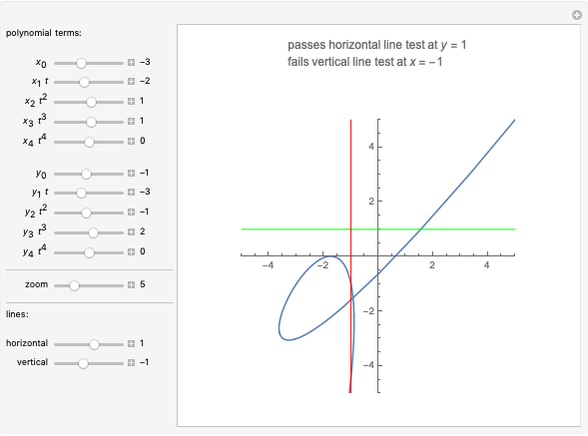
The graph of a function that is not identically zero is never symmetric with respect to the  axis as it necessarily fails the vertical line test (e.g.
axis as it necessarily fails the vertical line test (e.g. 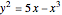 and
and 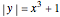 ). A function whose graph is symmetric with respect to the
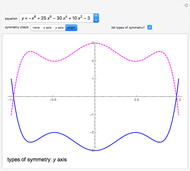
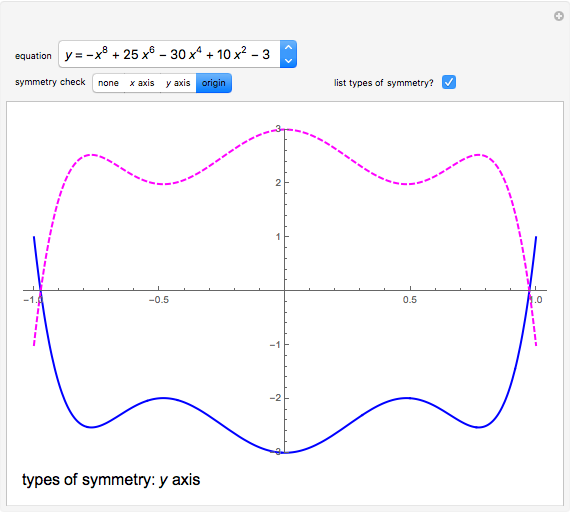
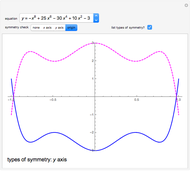
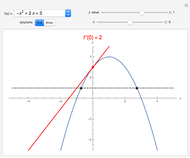
). A function whose graph is symmetric with respect to the 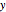 axis is called even (e.g.
axis is called even (e.g. 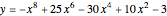 and
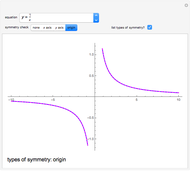
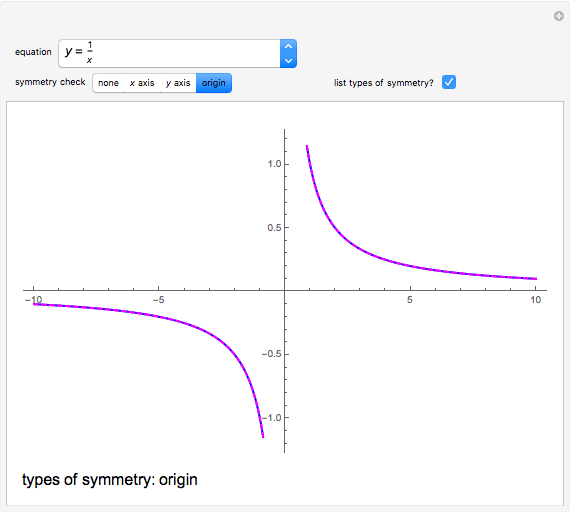
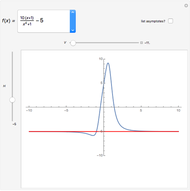
and 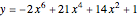 ). A function whose graph is symmetric with respect to the origin is called odd (e.g.
). A function whose graph is symmetric with respect to the origin is called odd (e.g. 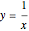 ).
).
Equations that are symmetric to both the  axis and
axis and 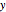 axis will necessarily also be symmetric with respect to the origin (e.g.
axis will necessarily also be symmetric with respect to the origin (e.g.  ). However, this is not a requirement for a graph to be symmetric with respect to the origin (e.g.
). However, this is not a requirement for a graph to be symmetric with respect to the origin (e.g. 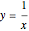 ).
).
Permanent Citation