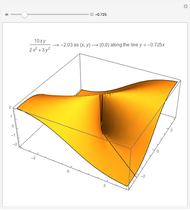
Intuition for the Fundamental Theorem of Calculus

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
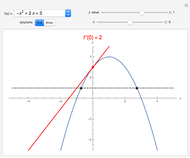
The fundamental theorem of calculus states that for a continuous function  on an interval
on an interval  , the integral is both continuous and differentiable on
, the integral is both continuous and differentiable on 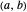 . More specifically, it states that
. More specifically, it states that  for all
for all 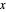 in
in  This Demonstration helps to provide the intuition behind this idea.
This Demonstration helps to provide the intuition behind this idea.
Contributed by: Laura R. Lynch (May 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Recall that the derivative of a function  is defined to be
is defined to be  . For arbitrarily small values of
. For arbitrarily small values of  , this says
, this says  , or (A)
, or (A) 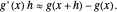
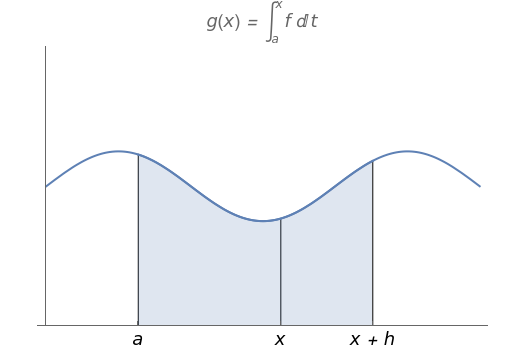
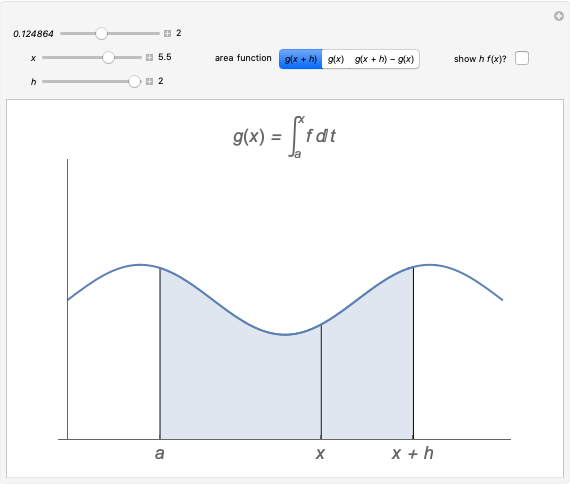
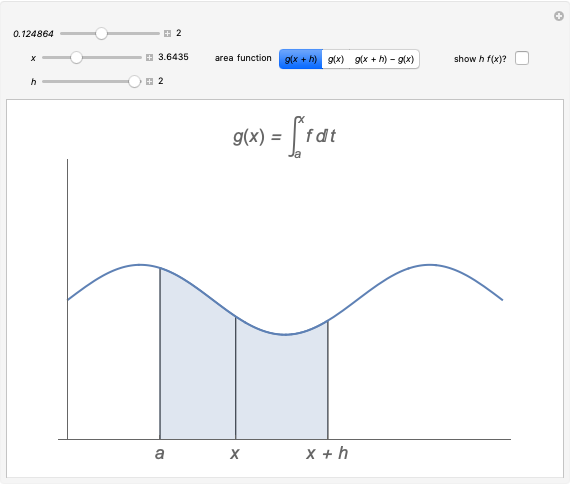
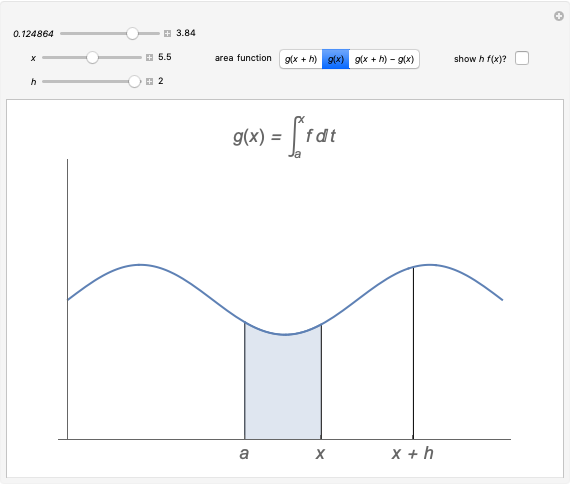
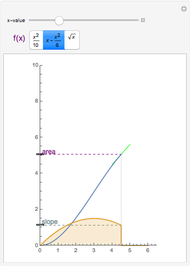
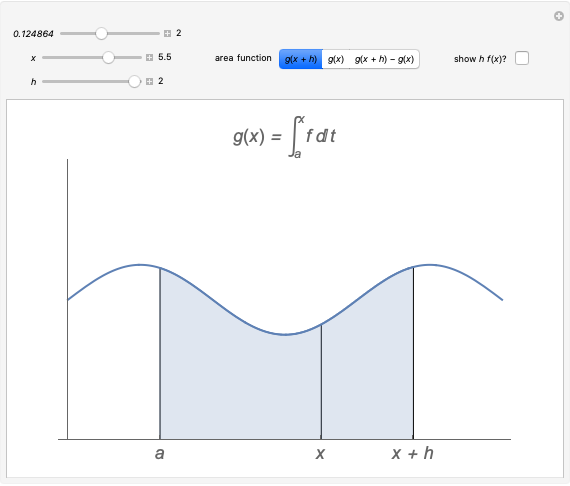
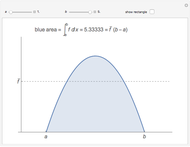
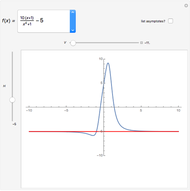
We use this idea to help develop the fundamental theorem of calculus. Define  to be the area function, that is,
to be the area function, that is,  . Then the Demonstration shows that
. Then the Demonstration shows that 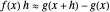 and so by (A),
and so by (A), 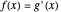 (since the approximation is in fact an equality as we take the limit as
(since the approximation is in fact an equality as we take the limit as  ). Thus
). Thus  is the derivative of the area function, that is,
is the derivative of the area function, that is,  as desired.
as desired.
Permanent Citation