Wolfram Demonstrations Project

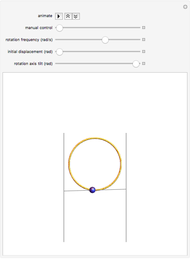
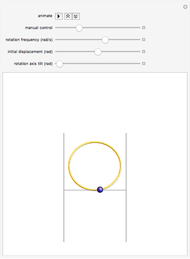
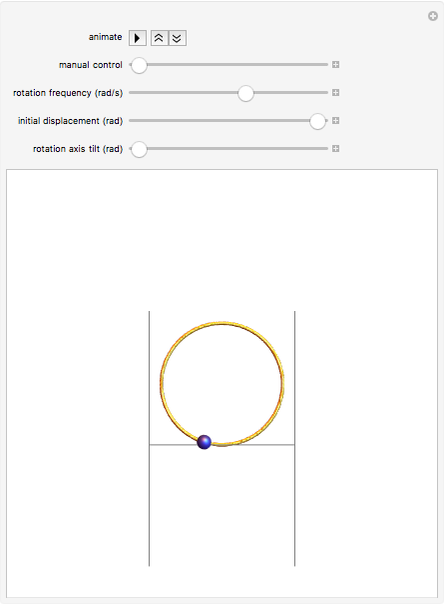
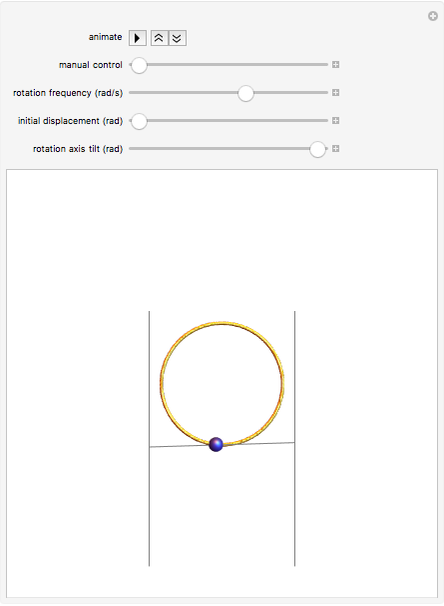
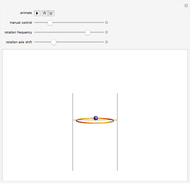
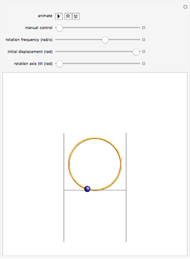
This Demonstration illustrates the behavior of a frictionless bead sliding on a circular hoop as the hoop is rotated about a horizontal axis tangent to the bottom of the hoop. Such a device can be built and used to illustrate the principle of the Paul rf ion trap. In the ideal case, the bead's motion is described exactly by Mathieu's equation. However, the behavior of the bead is very sensitive to small perturbations of the apparatus. In this Demonstration, you can observe the effect of increasing the initial displacement of the bead, as well as slightly tilting the rotation axis from the horizontal.

Contributed by: James A. Rabchuk

Rotate and Zoom in 3D
Slider Zoom
Automatic Animation

The hoop shown here has a radius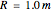

. Gravity is acting downward at

. The gray line indicates the horizontal axis of rotation. The motion of the bead is independent of its mass. The bead is given an initial displacement of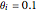

radians from the equilibrium point. Starting the Demonstration causes the hoop to rotate about the axis with angular frequency

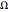, allowing the motion of the bead along the rotating hoop to be observed.

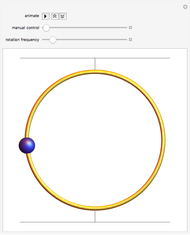
In the ideal case of small displacements from equilibrium and a perfectly horizontal axis of rotation, the motion of the bead can be described by Mathieu's equation, as discussed in the other Demonstration based on this model, Bead on a Horizontally Rotating Hoop with Movable Axis. With the axis of rotation as shown, the behavior of the bead is equivalent to the motion of an ion in an rf Paul trap. In the ideal case, the bead will remain trapped near the equilibrium point for rotational frequencies above 4.6 rad/s.

The transition from unstable motion to stable motion can be observed by using the scrollbar to vary the rotational frequency from 3 to 8 radians per second. The higher the rotational frequency above the minimum of 4.6 radians per second, the more slowly the bead oscillates about equilibrium. This is a characteristic feature of ponderomotive traps.

However, this trap is very sensitive to initial conditions. As the initial displacement is increased from the default value of 0.1 radians and the rotational frequency is increased, the bead can escape the trap. At higher frequencies, the bead experiences a significant "centrifugal force" pushing the bead away from equilibrium that can destabilize the motion.

The motion of the bead is also very sensitive to any tilt in the axis of rotation, corresponding to the case when the apparatus is not perfectly leveled. Tilting causes the bead to experience a small centrifugal force pushing it along the tilted axis down from the original equilibrium point. For very small tilts, the bead remains trapped at moderate rotational frequencies, but escapes at higher frequencies. For slightly larger tilts, the bead can no longer be trapped. This behavior can be explored by adjusting the tilt angle from 0 to 0.03 radians (1.7 degrees).

Reference: A. K. Johnson and J. A. Rabchuk, "A Bead on a Hoop Rotating about a Horizontal Axis: A One-Dimensional Ponderomotive Trap," (accepted for publication by the American Journal of Physics).

"Bead on a Horizontally Rotating Hoop: Variable Initial Displacement and Tilted Axis" from the Wolfram Demonstrations Project
http://demonstrations.wolfram.com/BeadOnAHorizontallyRotatingHoopVariableInitialDisplacementAn/

Contributed by: James A. Rabchuk