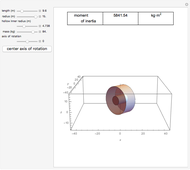
Bead on a Horizontally Rotating Hoop with Movable Axis

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
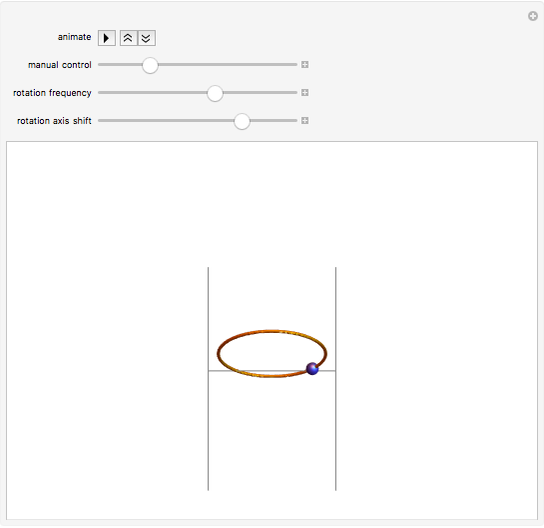
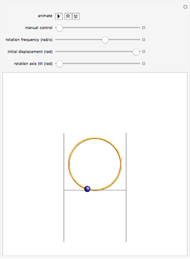
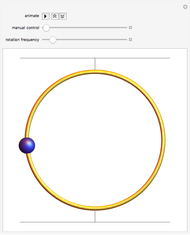
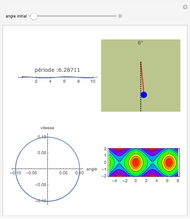
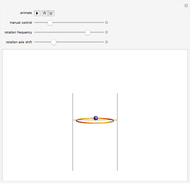
This Demonstration illustrates the behavior of a bead sliding with very minimal friction on a circular hoop as the hoop is rotated about a horizontal axis that can be shifted up or down. The behavior of the bead in the rotating frame of the hoop illustrates the principle of ponderomotive traps, such as the Paul rf trap and the Penning trap, used in atomic and molecular physics. Such traps display parametric stability, so that the particle is kept near its equilibrium position only for certain values of the parameters. In this Demonstration the variable parameters are the frequency of rotation and the vertical shift of the axis of rotation.
Contributed by: James A. Rabchuk (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The hoop shown here has a radius 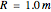 . Gravity is acting downward at
. Gravity is acting downward at 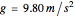 . The friction coefficient is 0.001. The gray line indicates the horizontal axis of rotation. The motion of the bead is independent of its mass. The bead is given an initial displacement of 0.10 radians from the equilibrium point. Starting the Demonstration causes the hoop to rotate about the axis with angular frequency
. The friction coefficient is 0.001. The gray line indicates the horizontal axis of rotation. The motion of the bead is independent of its mass. The bead is given an initial displacement of 0.10 radians from the equilibrium point. Starting the Demonstration causes the hoop to rotate about the axis with angular frequency 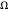 , allowing the motion of the bead along the rotating hoop to be observed.
, allowing the motion of the bead along the rotating hoop to be observed.
For small oscillations, the motion of the bead is described by Mathieu's equation for the angle of displacement,  ,
,
 ,
,
where 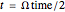 is the time scaled by the frequency of rotation, and
is the time scaled by the frequency of rotation, and  and
and  are real constants fixed by the parameters in the problem. For the bead on the hoop,
are real constants fixed by the parameters in the problem. For the bead on the hoop,
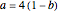 ,
,
where  is the amount the axis of rotation is shifted down from the center, and
is the amount the axis of rotation is shifted down from the center, and
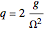 .
.
Solutions to Mathieu's equation display parametric stability, so that the amplitude of the motion remains bounded for certain values of  and
and  , but unbounded for others. Friction tends to increase the stability of the motion. When the square of the rotational frequency is very large compared to
, but unbounded for others. Friction tends to increase the stability of the motion. When the square of the rotational frequency is very large compared to  , such that
, such that  is nearly zero, the motion is stable for all values of
is nearly zero, the motion is stable for all values of  , except when
, except when  . On the other hand, when
. On the other hand, when  is very large, corresponding to low frequencies of rotation, the motion is always unstable.
is very large, corresponding to low frequencies of rotation, the motion is always unstable.
In this Demonstration, you can vary the rotation frequency from 3 to 8 radians per second. The lowest frequency of 3 radians per second leads to instability in all cases. As the frequency is increased, the bead tends to be "trapped" near the equilibrium point. In the limit that 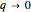 , Mathieu's equation predicts that the motion will become essentially harmonic. However, at very large frequencies and sufficiently large initial displacements, the motion is no longer accurately described by a Mathieu equation and the bead experiences a significant "centrifugal force". This behavior is further explored in another Mathematica Demonstration based on this model, Bead on a Horizontally Rotating Hoop: Variable Initial Displacement and Tilted Axis.
, Mathieu's equation predicts that the motion will become essentially harmonic. However, at very large frequencies and sufficiently large initial displacements, the motion is no longer accurately described by a Mathieu equation and the bead experiences a significant "centrifugal force". This behavior is further explored in another Mathematica Demonstration based on this model, Bead on a Horizontally Rotating Hoop: Variable Initial Displacement and Tilted Axis.
Shifting the axis of rotation down from the center of the hoop changes the value of the other Mathieu parameter,  . The motion when
. The motion when  and
and 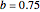 (
(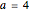 and
and 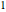 , respectively) is predicted by the Mathieu equation to be unstable always. However, for the case
, respectively) is predicted by the Mathieu equation to be unstable always. However, for the case  , after a small increase in the amplitude of the motion the centrifugal force acts to stabilize the motion. On the other hand, when
, after a small increase in the amplitude of the motion the centrifugal force acts to stabilize the motion. On the other hand, when 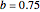 , the motion of the bead is always unstable, no matter what the rotational frequency. When the axis is tangent to the bottom of the hoop (
, the motion of the bead is always unstable, no matter what the rotational frequency. When the axis is tangent to the bottom of the hoop (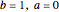 ) the motion of the bead is equivalent to that of an ion in a Paul rf trap.
) the motion of the bead is equivalent to that of an ion in a Paul rf trap.
Reference: A. K. Johnson and J. A. Rabchuk, "A Bead on a Hoop Rotating about a Horizontal Axis: A One-Dimensional Ponderomotive Trap," (accepted for publication by the American Journal of Physics).
Permanent Citation