Levich Equation for Rotating Disk Electrode

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
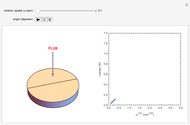
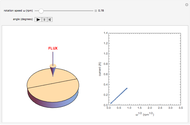
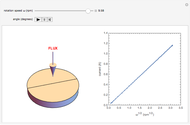
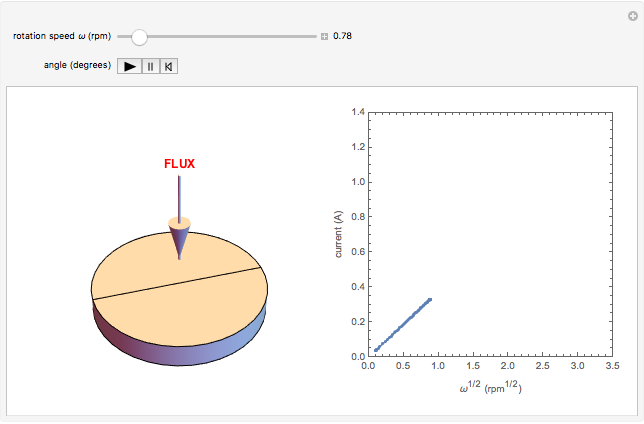
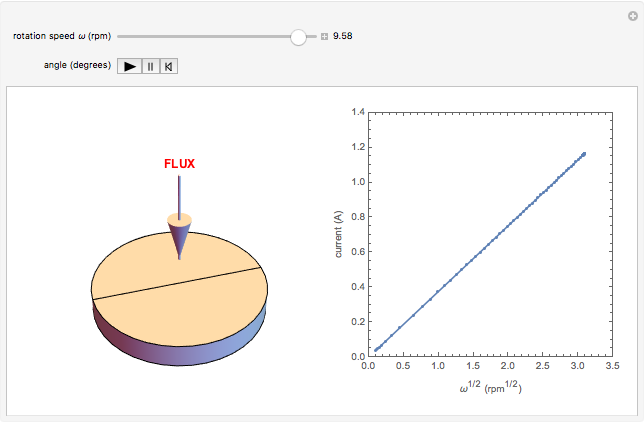
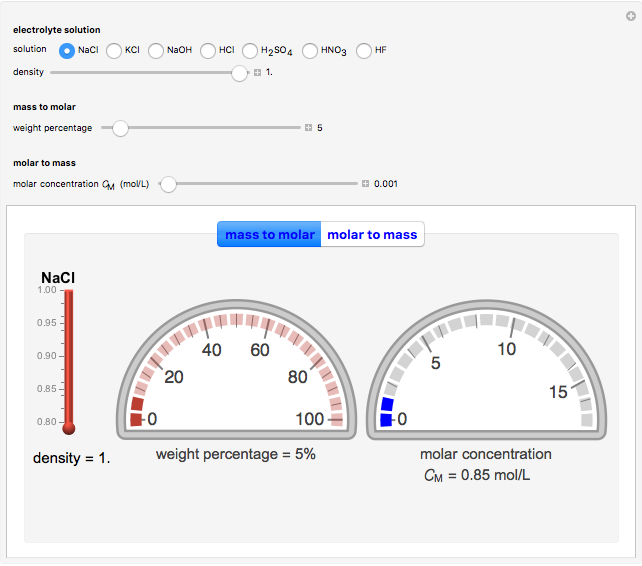
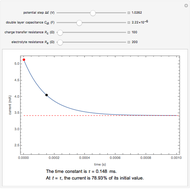
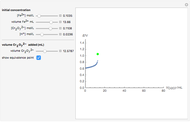
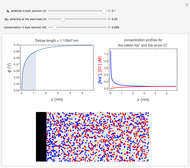
The Levich equation models the variation of diffusion and solution flow around a rotating disk electrode (RDE). This Demonstration shows the dependence of the current on the rotation speed.
Contributed by: Quang-Dao Trinh (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
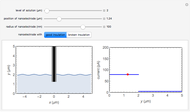
In a rotating disk electrode, the electrolytes are made to flow past the electrode by convection. In this Demonstration, when the rotation speed increases, the flux of electroactive species to the surface of the electrode increases by convection (shown by the red arrow) and the current increases.
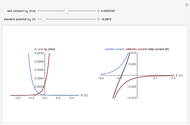
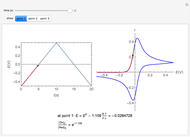
The Levich equation predicts the current observed at a rotating disk electrode and shows that the current is proportional to the square root of rotation speed. The equation is
 , where
, where
 is the current limited in voltammogram (A),
is the current limited in voltammogram (A),
 is the number of electrons transferred,
is the number of electrons transferred,
 is the Faraday constant (C/mol),
is the Faraday constant (C/mol),
 is the electrode area (
is the electrode area ( ),
),
 is the diffusion coefficient
is the diffusion coefficient  /s),
/s),
 is rotation speed (radian/sec),
is rotation speed (radian/sec),
 is the kinematic viscosity of the solution
is the kinematic viscosity of the solution  /sec), and
/sec), and
 is the concentration of the electroactive species
is the concentration of the electroactive species  ).
).
The Levich equation can be used to calculate the diffusion coefficient  as a function of the rotation speed
as a function of the rotation speed  and the current
and the current  .
.
Reference
[1] J. Wang, Analytical Electrochemistry, 3rd ed., New York: John Wiley & Sons, 2006.
Permanent Citation