Wolfram Demonstrations Project

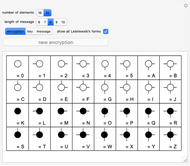
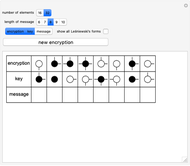
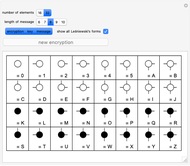
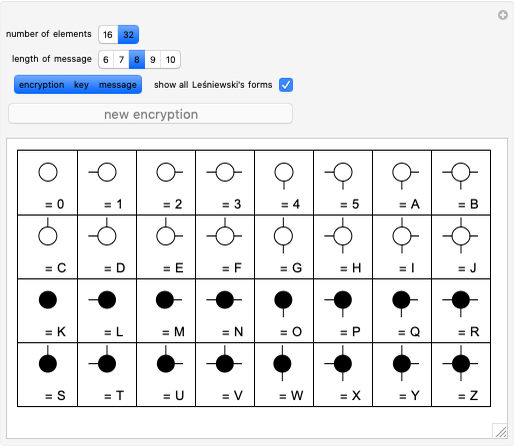
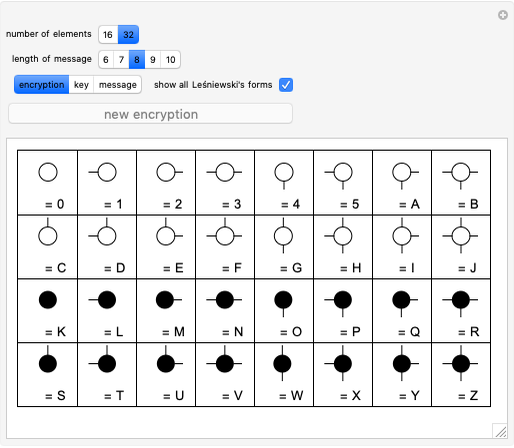
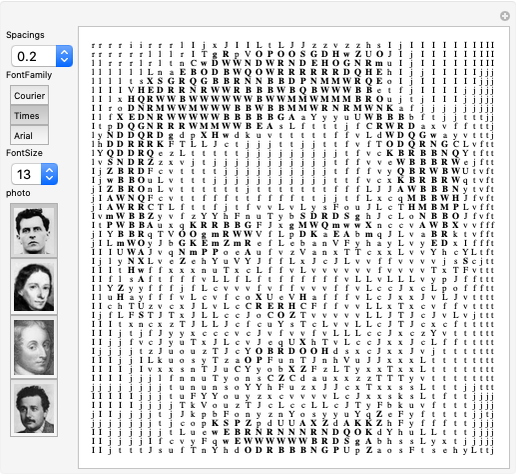
This Demonstration shows an encryption code based on Leśniewski's 16 Boolean ring forms for propositional functions of two arguments, also extended to 32 elements using filled circles. A plaintext consists of a sequence of elements from a Boolean ring and is encrypted using another sequence (the key) of the same length. Suppose the corresponding elements at position

are

and

; then the corresponding element of the encryption is

. A receiver then decrypts the plaintext using the key:

Contributed by: Izidor Hafner

Leśniewski, Mazurkiewicz and Sierpiński helped the Polish army decode Soviet military communications. Their work was instrumental in the decisive 1920 defeat of Soviet invading forces in the suburbs of Warsaw [1].

Reference

[1] A. McFarland, J. McFarland and J. T. Smith, eds., Alfred Tarski, Early Work in Poland: Geometry and Teaching, New York: Birkhäuser, 2014 p. 9.