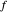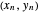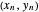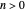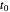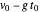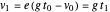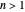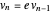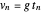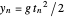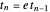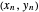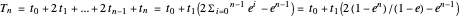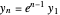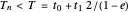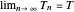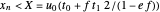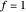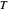Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Bounce Time for a Bouncing Ball

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

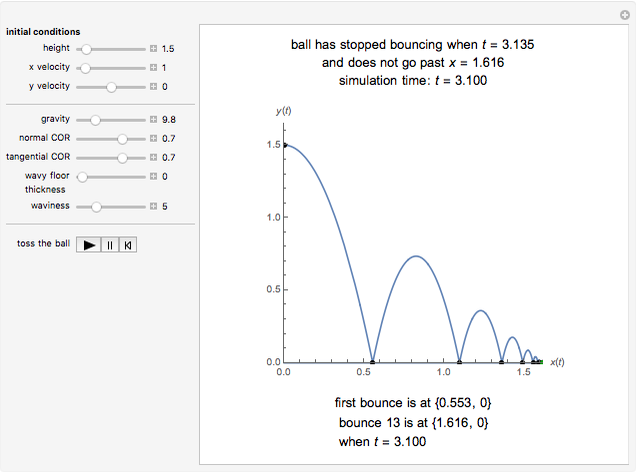
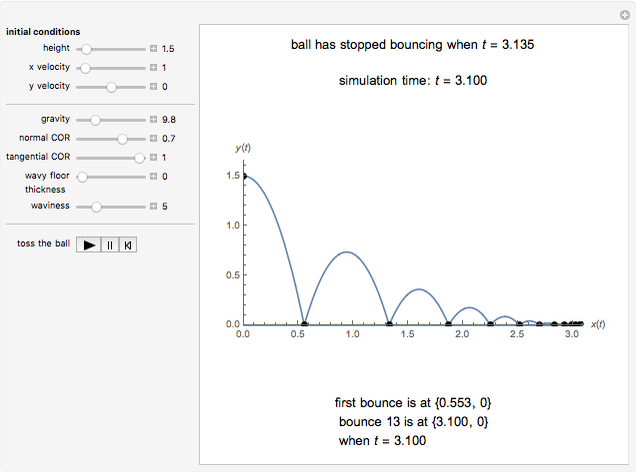
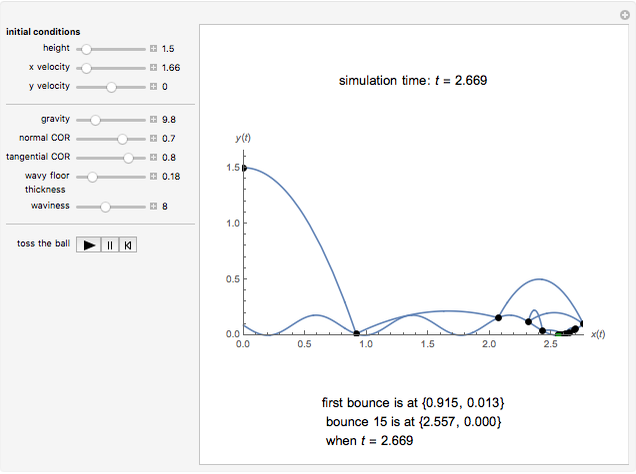
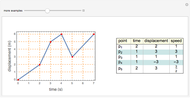
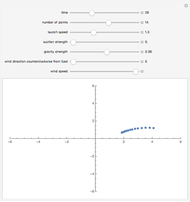
Click "toss the ball" for an animation. Initially, the ball is tossed horizontally with speed 1 m/s from a height of 1.5 m onto a flat floor. The ball has normal and tangential coefficients of restitution of 0.7 and 0.8. (That means the normal and tangential speeds are reduced by factors of 0.7 and 0.8 at each bounce.) It takes 3.10 seconds for the ball to bounce 13 times, and then it has moved horizontally 1.96 m. The formulas below show the ball has finished bouncing at time 3.135, and it is stopped at (1.96, 0).

[more]

After the first toss, the path and bounce points of the ball are displayed, and change as controls are varied. The bounce time and final position are shown when the floor is flat. If "wavy floor thickness" is positive, the ball lands on a wavy surface, and you can adjust the waviness.

It is surprising that if the normal and tangential coefficients of restitution and satisfy and , then the ball will come to rest in finite time. We compute the stopping time and final ball position for a flat floor.

Suppose the ball is tossed onto a flat floor from , where and , with initial velocity , where , and assume zero turnaround time.

Let be the ball's velocity at the rebound and let be the coordinates of the ball at its maximum height after the bounce, . Let be the time of the first bounce, and let be the time it takes the ball to fall from to the floor, .

Then satisfies and the vertical velocity at is . Thus and . Also, and . For , , , , , and . Hence and for .

Therefore, , .

For , the ball is at at time ,, and .

Thus, and . Also, and .

It follows that the ball is stopped at at time . If the floor is frictionless and , the ball has ceased bouncing at time , but continues sliding with speed .

[less]

Contributed by: Roger B. Kirchner (February 2010)
Based on programs by: Enrique Zeleny, Rob Morris, and Oleksandr Pavlyk
Open content licensed under CC BY-NC-SA

Snapshots

Details

The program for computing the bouncing ball's path is adapted from the bouncing ball example in the Mathematica tutorial "EventLocator" Method for NDSolve, and Enrique Zeleny's Demonstration Stroboscopic Photograph of a Bouncing Ball.

The program for animating the ball is adapted from Rob Morris and Oleksandr Pavlyk's Demonstration Animated Projectile Motion.

The bouncing ball program assumes that if the tangential and normal components of velocity are and before a bounce, they are 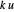and after the bounce, where . We have generalized so the reflected components are 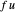and -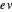, where we call the tangential coefficient of restitution and the normal coefficient of restitution. There may be a reason to assume 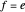, but is the usual coefficient of restitution, and 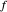seems to be a frictional effect. Of course, friction would affect rotation, which we ignore.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send