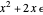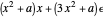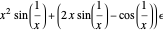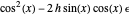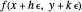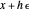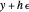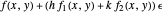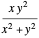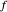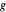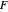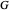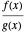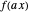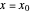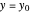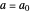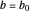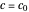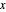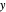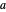Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Automatic Differentiation

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

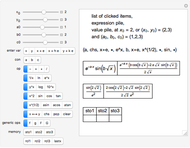
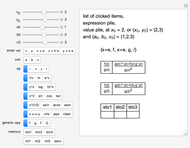
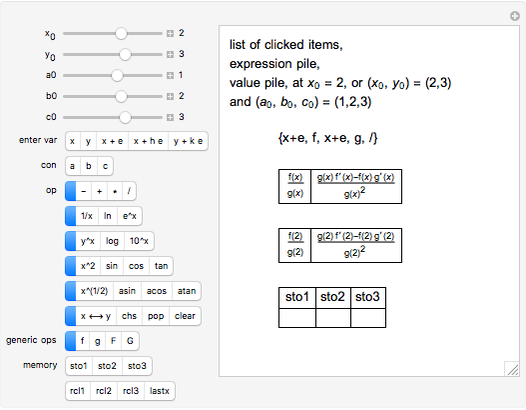
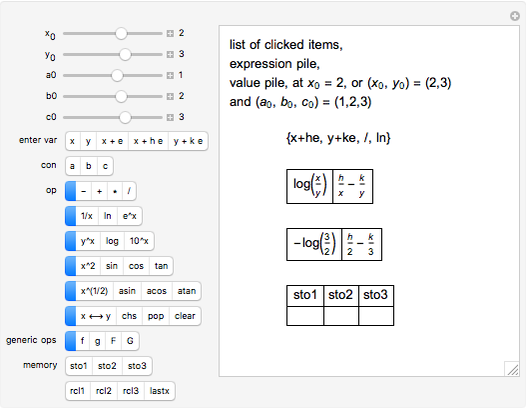
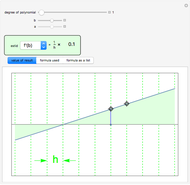
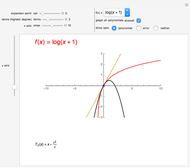
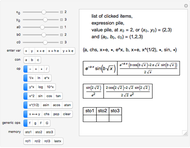
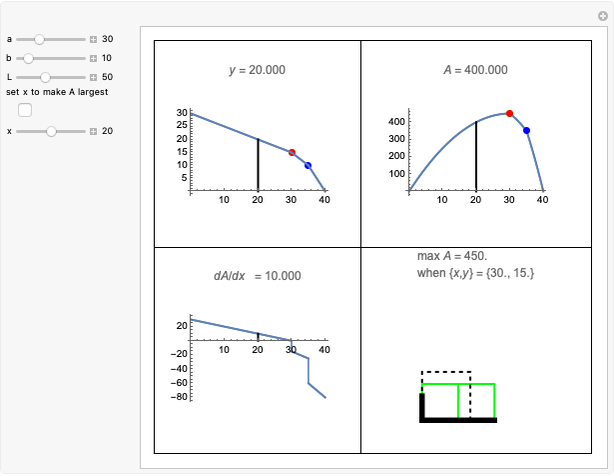
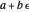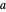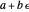This is a dual number expression RPN (reverse Polish notation) calculator for automatic differentiation, modeled on an old-style scientific calculator. Dual numbers are numbers of the form , where , are real and . ( is displayed with 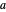and in adjacent boxes. Use the calculator to calculate an arithmetic expression in 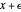and reals 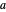, , and ). Clicking a value puts the value on top of a pile. Clicking an "op" applies the "op" to the top member(s) of the pile as argument(s), and replaces them on the pile with its value. This is the RPN method of evaluation. The list of buttons clicked will be the reverse Polish notation for the expression. If the result is 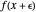for a function 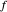, its value will be 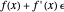. Thus, 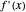is calculated "automatically". Moreover, this will be the result if 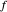is any function computable by the calculator. In fact, 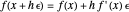. It is as if 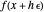were expanded in a Maclaurin series in , since .

[more]

Click "x + e", "x + e", "*" to get .

Click "x + e", "x + e", *, "a", +, "x + e", "*" to get .

Click "x + e", "x^2", "x + e", "1/x", "sin", "*" to get .

Click "x + h e", "cos", "x^2" to get .

Calculating an expression in dual numbers and results in .

For example, to compute the partial derivatives of , click "x + h e", "y + k e", "x^2", "*", "x + h e", "x^2", "y + k e", "x^2", "+", "/". The partial derivatives are the coefficients of and in the second box.

Built-in generic functions and of one variable and and of two variables can be used to derive general differentiation formulas.

For example, compute the formula for the derivative of by clicking "x + e", "f", "x + e", "g", "/" and for by clicking "a", "x + e", "*", "f".

The expression pile contains symbolic expressions and the value pile contains these expressions evaluated at , , , , and . (To get decimal values, set an involved slider to a decimal value.) Click "clear" to start a new calculation. The calculator can also be used to calculate real expressions and their values in , , , , and .

[less]

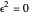Contributed by: Roger B. Kirchner (September 2009)
Open content licensed under CC BY-NC-SA

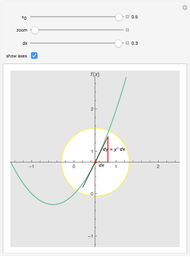
Snapshots

Details

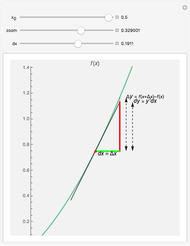
The calculator works by extending built-in functions 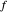of one or two real variables to duals by 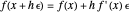and 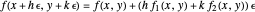. The chain rule implies these relations hold for every computable function.

For example, if 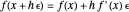and 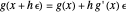, then .

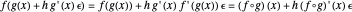In Dual Number (Wolfram MathWorld), a dual number is a number of the form 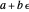, where 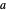and are real, and is a matrix such that , such as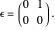

Our calculator represents the dual number 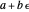as the expression 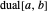, with operations defined by

,

,

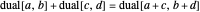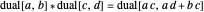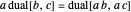, which defines negation (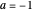) and hence subtraction,

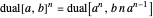for real 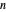, which defines reciprocal (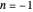) and hence division,

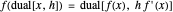, for functions 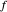of one variable,

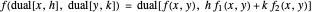for functions of two variables,

.

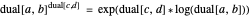These rules are implemented in Mathematica using "up values". With operations thus overloaded, the calculator is implemented as if it were defined only for reals.

References

[1] D. Piponi, "Automatic Differentiation". A Neighborhood of Infinity. (Jul 28, 2005) blog.sigfpe.com/2005/07/automatic-differentiation.html.

[2] L. B. Rall, "The Arithmetic of Differentiation," Mathematics Magazine, 59(5), 1986, pp. 275–282.

[3] R. D. Neidinger, "Automatic Differentiation and APL," The College Mathematics Journal, 20(3), 1989 pp. 238–251.

[4] R. D. Neidinger, "Introduction to Automatic Differentiation and MATLAB Obect Oriented Programming," SIAM Review, 52(3), 2010 pp. 545–563.

Also see the Wikipedia entries for Dual number and Automatic differentiation.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send