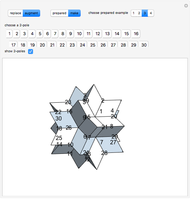
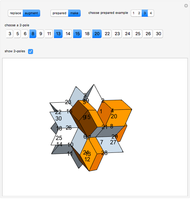
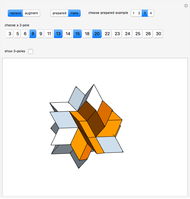
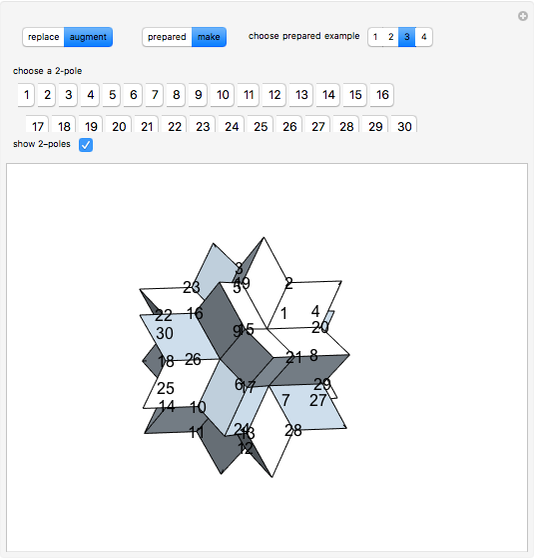
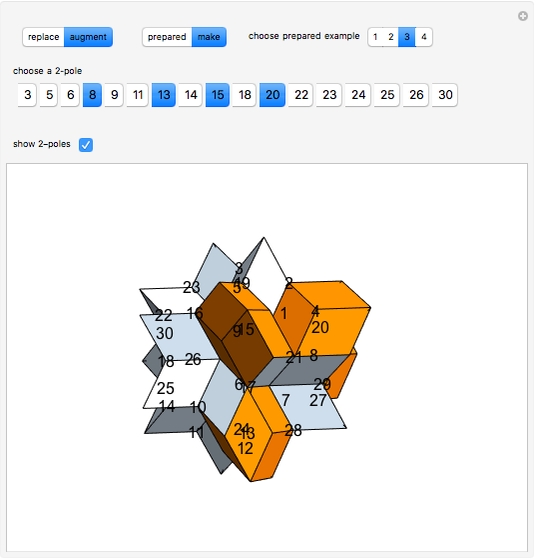
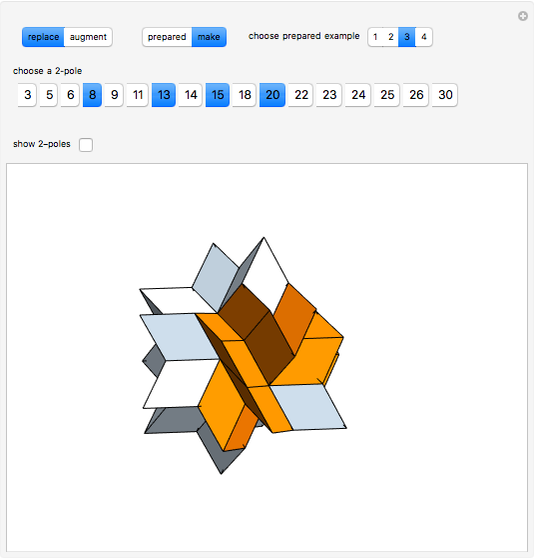
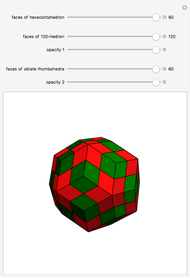
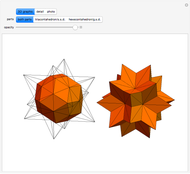
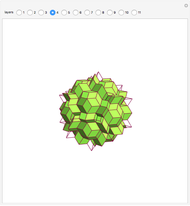
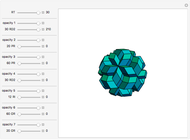
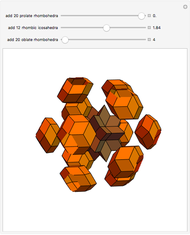
The rhombic hexecontahedron consists of 20 acute golden rhombohedra. Its symmetry group is icosahedral, so there are 15 axes of 2-fold rotational symmetry. Two points where an axis of -fold rotational symmetry punctures the surface of a polyhedron are called -poles. So the hexecontahedron has 30 2-poles, which are shown in the controls. Choosing from them using the numbered buttons, you can replace two acute rhombohedra that are adjacent to a 2-pole by two obtuse rhombohedra, or alternatively, you can augment the polyhedron by two obtuse rhombohedra. When you click a number, the buttons that correspond to adjacent 2-poles disappear, because these poles are no longer in play. This Demonstration also shows four prepared examples.