Complex Zeros of Quadratic Functions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
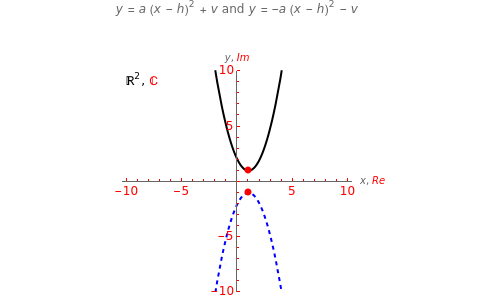
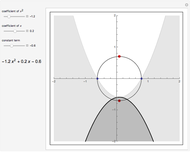
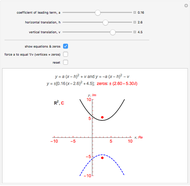
This Demonstration shows the graphs of two symmetric quadratic functions (with respect to the  axis) of the form
axis) of the form 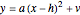 and
and  , where
, where  and
and  are the horizontal and vertical translations of the corresponding parabolas
are the horizontal and vertical translations of the corresponding parabolas 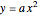 and
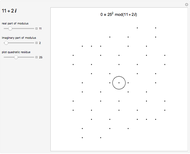
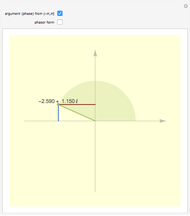
and 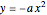 , with vertices at the origin. Their complex zeros are identical and marked by red dots located in the complex plane
, with vertices at the origin. Their complex zeros are identical and marked by red dots located in the complex plane  , where the
, where the  and
and 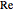 axes (labeled in red on the graph) coincide with the Cartesian plane
axes (labeled in red on the graph) coincide with the Cartesian plane 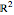 coordinate
coordinate  and
and  axes; that is, the
axes; that is, the  axis is also the real axis and the
axis is also the real axis and the  axis is also the imaginary axis. While any real zeros lie on the
axis is also the imaginary axis. While any real zeros lie on the  axis (or real axis), imaginary zeros come in pairs (complex conjugates) and lie on the vertical line
axis (or real axis), imaginary zeros come in pairs (complex conjugates) and lie on the vertical line  that runs through the vertices (and foci) of the parabolas. Further, as complex conjugates, the zeros are symmetric with respect to the
that runs through the vertices (and foci) of the parabolas. Further, as complex conjugates, the zeros are symmetric with respect to the  axis (real axis). To see the effects on the graph when
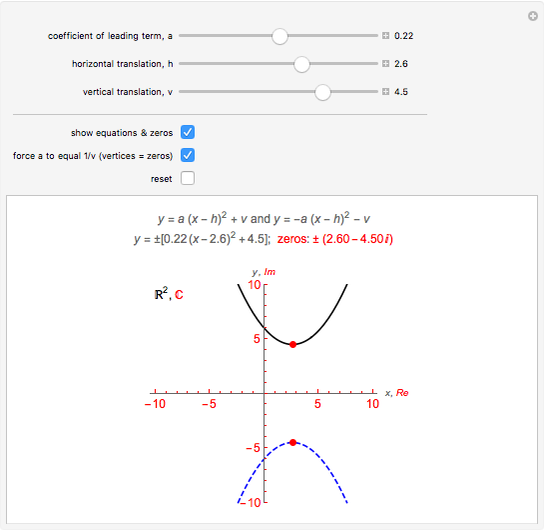
axis (real axis). To see the effects on the graph when 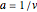 , click on the checkbox "force
, click on the checkbox "force  to equal
to equal  (vertices = zeros)" and move the
(vertices = zeros)" and move the  slider.
slider.
Contributed by: Barry Cherkas (March 2011)
(Hunter College and WebGraphing.com)
Open content licensed under CC BY-NC-SA
Snapshots
Details
To find the complex zeros, set  in each equation,
in each equation, 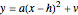 and
and  , and solve for
, and solve for  :
: 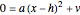 and
and 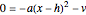 , which implies (in either case)
, which implies (in either case) 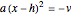 ,
,  ,
, 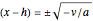 ,
, 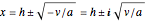 . When
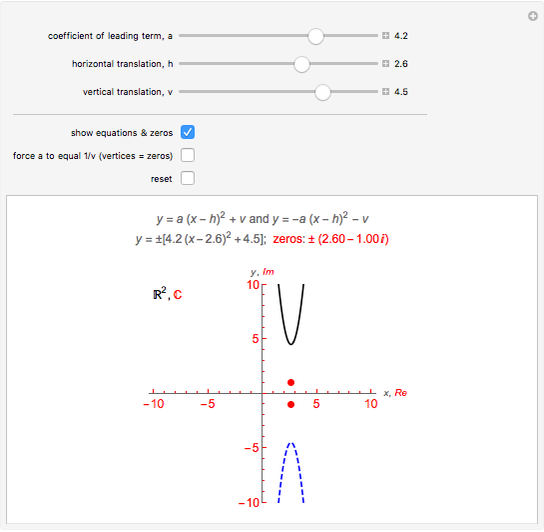
. When 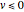 , the zeros are real and lie on the
, the zeros are real and lie on the  axis; when
axis; when  , there are two imaginary zeros (complex conjugates) that lie on the vertical line
, there are two imaginary zeros (complex conjugates) that lie on the vertical line  . For
. For  and fixed vertices
and fixed vertices 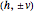 , observe that: (1) as
, observe that: (1) as 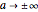 , the parabolas get narrower while the imaginary zeros approach the real axis along the line
, the parabolas get narrower while the imaginary zeros approach the real axis along the line  ; and (2) as
; and (2) as 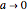 , the parabolas flatten out while the imaginary zeros approach ±
, the parabolas flatten out while the imaginary zeros approach ±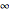 along the line
along the line  . When
. When  and the imaginary part of either imaginary zero is the same as
and the imaginary part of either imaginary zero is the same as  , that is when
, that is when 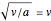 , both imaginary zeros coincide with the vertices. To solve
, both imaginary zeros coincide with the vertices. To solve 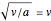 , square both sides and get
, square both sides and get  , which has solution
, which has solution 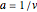 .
.
Permanent Citation