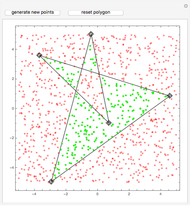
Component Identification and Boundary Delineation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
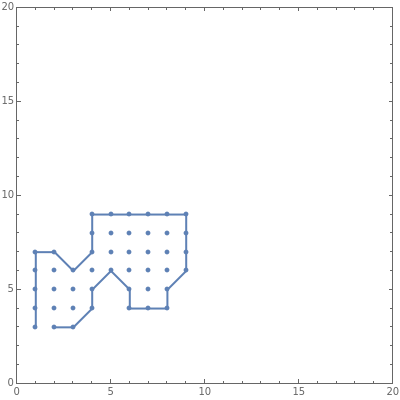
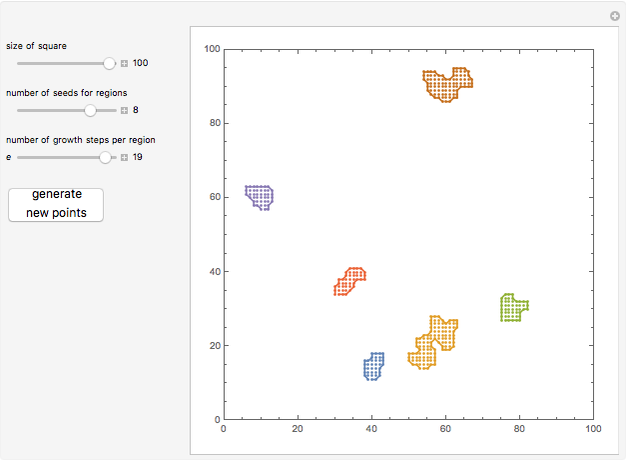
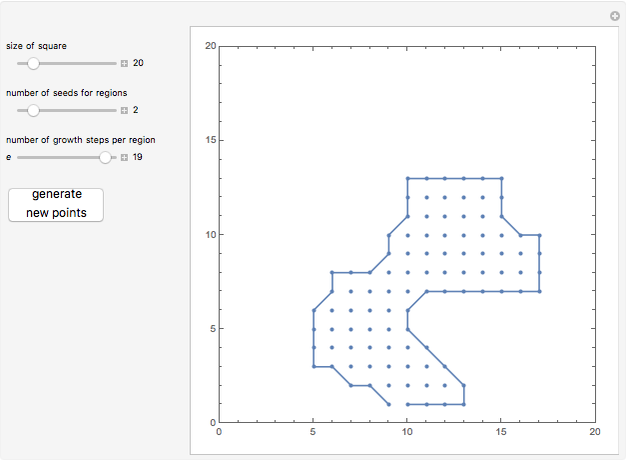
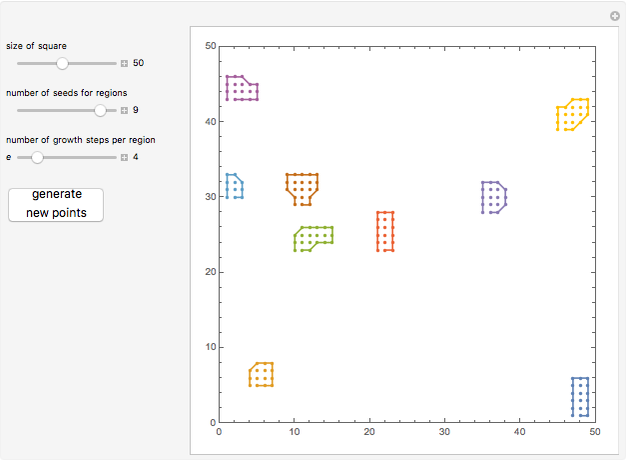
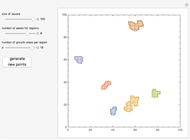
Morphological component identification and boundary delineation are important problems. For a given square grid, based on some thresholding, we want to find the separate components and their boundaries. This Demonstration implements the "one component at a time" marching squares method for the former and the Moore boundary tracing algorithm for the latter. A step before showing this is to first create some artificial regions. For this, the Moore neighborhood is itself used in a nested fashion on a set of seed points.
Contributed by: Raja Kountanya (February 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A set of points is given in an 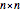 square grid. A Moore window around a point is the list of eight points surrounding it, corresponding to its NW, N, NE, E, SE, S, SW, and W neighbors. To illustrate the component identification and boundary delineation, it is important to construct some artificial components first. To do this, points from the Moore windows of a set of randomly chosen seeds are added to form a new set. Then more points from Moore windows of random points of this set are added. As this process is applied
square grid. A Moore window around a point is the list of eight points surrounding it, corresponding to its NW, N, NE, E, SE, S, SW, and W neighbors. To illustrate the component identification and boundary delineation, it is important to construct some artificial components first. To do this, points from the Moore windows of a set of randomly chosen seeds are added to form a new set. Then more points from Moore windows of random points of this set are added. As this process is applied  times and duplicate copies are deleted each time, the set grows into multiple windows of random shapes.
times and duplicate copies are deleted each time, the set grows into multiple windows of random shapes.
The morphological component identification is performed with the routines BottomLeftPoint, RetWindow, and AllWindows.
As the name suggests, the BottomLeftPoint returns the point in the bottom-left portion of the list. The RetWindow routine takes a list of points and returns the first connected component or window. It works according to the ”one component at a time” method given in [1], using buffer, window, and total stacks to track the points in a binary search scheme.
Define the total stack to be the complete set of points (from all windows). Let  denote the point at the bottom left. Add
denote the point at the bottom left. Add  to the buffer stack. Let
to the buffer stack. Let 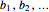 be the connected members of
be the connected members of  in the Moore window. Add them to the buffer stack with
in the Moore window. Add them to the buffer stack with  as the first member to get
as the first member to get 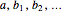 . Also add
. Also add  to the window stack, drop
to the window stack, drop  from the buffer, and drop
from the buffer, and drop 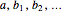 from the total stack. Next, look for members connected to
from the total stack. Next, look for members connected to  ; call them
; call them 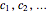 and add them to the buffer stack. As before, add
and add them to the buffer stack. As before, add  to the window stack, drop
to the window stack, drop  from the buffer stack to get
from the buffer stack to get 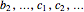 , and drop
, and drop 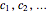 from the total stack.
from the total stack.
Progressing like this sequentially, all members of a single window are identified using "marching squares." It is important that this routine be coded optimally to minimize the number of comparisons, unions, complements, etc. The AllWindows routine takes the complete set of data and returns all the windows.
The boundary delineation is performed with the routines ClkRot, BottomLeftPoint, and Bdry.
The Bdry routine takes the map given by indices and computes the boundary using Moore’s algorithm (given in [2]). It uses the function ClkRot for clockwise rotation of neighborhood points. The function resembles a wheel spinning in the clockwise direction at each point on the boundary, using the backtracking variable  . It starts from the point at the bottom left in the window. As a side benefit, the returned boundary is also ordered in the clockwise orientation.
. It starts from the point at the bottom left in the window. As a side benefit, the returned boundary is also ordered in the clockwise orientation.
In the Demonstration, choose settings and generate points to see how the different components are identified and boundaries drawn. You can also notice that if the seeds are closely located, with adequate expansions, the components coalesce, yielding a single boundary.
References
[1] Wikipedia. "Connected-Component Labeling." (Jan 27, 2015) en.wikipedia.org/wiki/Connected-component_labeling.
[2] Wikipedia. "Moore Neighborhood." (Jan 27, 2015) en.wikipedia.org/wiki/Moore_neighborhood.
Permanent Citation