Yield under a Rigid Toroidal Indenter

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
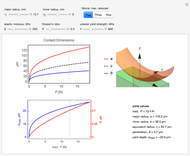
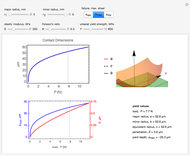
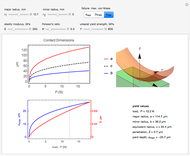
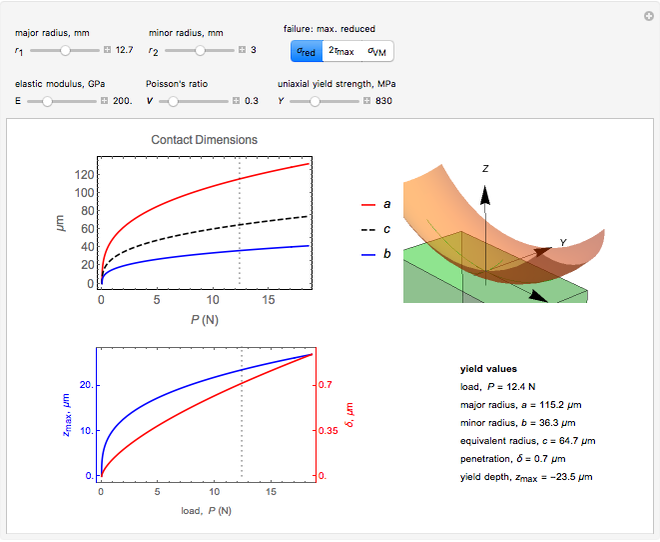
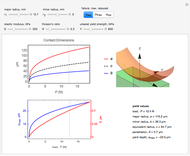
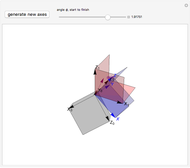
This Demonstration allows you to simulate frictionless contact of a rigid toroidal indenter on the surface of an elastic half-space and to determine parameters for initial yield.
Contributed by: Raja Kountanya (September 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Consider a rigid toroidal indenter with principal radii  and
and  ,
,  , pressing against an elastic semi-infinite body of elastic modulus (Young's modulus)
, pressing against an elastic semi-infinite body of elastic modulus (Young's modulus)  and yield strength
and yield strength  with a force
with a force  only along the
only along the  axis, and without friction. Let the major and minor radius of the contact ellipse be
axis, and without friction. Let the major and minor radius of the contact ellipse be  and
and  , respectively. The eccentricity of the contact ellipse
, respectively. The eccentricity of the contact ellipse  is independent of the load [1, 2] and is given by the solution to the following equation. Note that when
is independent of the load [1, 2] and is given by the solution to the following equation. Note that when  , the contact patch is circular:
, the contact patch is circular:  and
and  .
.
 .
.
Here  and
and  are the complete elliptic integral functions. Let
are the complete elliptic integral functions. Let  . For given
. For given  , we can find the geometric mean radius
, we can find the geometric mean radius  , penetration
, penetration  and maximum pressure
and maximum pressure  using formulas in Johnson [1]. We can calculate
using formulas in Johnson [1]. We can calculate  and
and  .
.
 ,
,
 ,
,
 .
.
As the load is increased, at a certain point along the  axis and under the indenter, the material will yield. Since the shear stress components in the coordinate system chosen vanish by symmetry, the normal stresses become the principal stresses. Then, the location of initial yield can be predicted using one of three common criteria: maximum reduced stress, shear stress or von Mises stress.
axis and under the indenter, the material will yield. Since the shear stress components in the coordinate system chosen vanish by symmetry, the normal stresses become the principal stresses. Then, the location of initial yield can be predicted using one of three common criteria: maximum reduced stress, shear stress or von Mises stress.
The formulas for the normal stresses along the  axis are given in [1]. In the following,
axis are given in [1]. In the following,  and over-bar represents values normalized by
and over-bar represents values normalized by  , for example,
, for example,  . When
. When  , the formulas for the normal (principal) stresses
, the formulas for the normal (principal) stresses  ,
,  ,
,  are tedious to calculate [1, 2].
are tedious to calculate [1, 2].
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
When the toroidal indenter becomes spherical, the normal (principal) stress components  ,
,  and
and  are given by
are given by
 ,
,
 .
.
To facilitate comparison with given yield strength  of the material, we can write the following formulas.
of the material, we can write the following formulas.
 where
where  ,
,
 ,
,
 .
.
Writing  , the three failure criteria can be written as: reduced stress (
, the three failure criteria can be written as: reduced stress ( ), shear stress
), shear stress  ) and von Mises stress
) and von Mises stress  ). Solving for the location of initial yield below the indenter
). Solving for the location of initial yield below the indenter  using the Mathematica function FindMaximum, we obtain
using the Mathematica function FindMaximum, we obtain  from
from  .
.
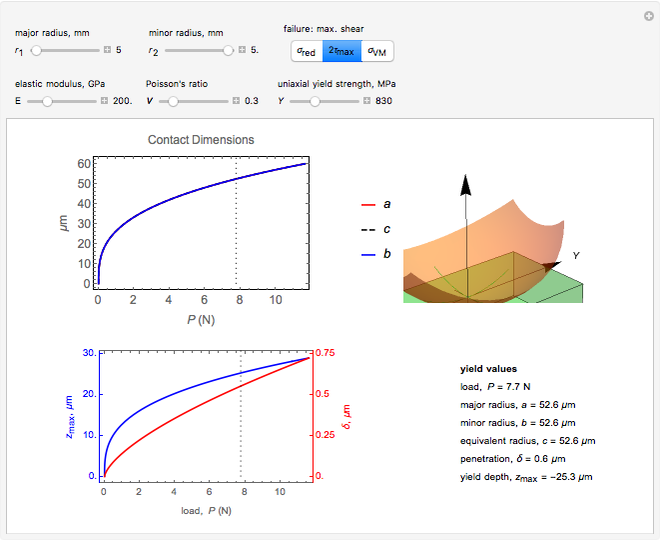
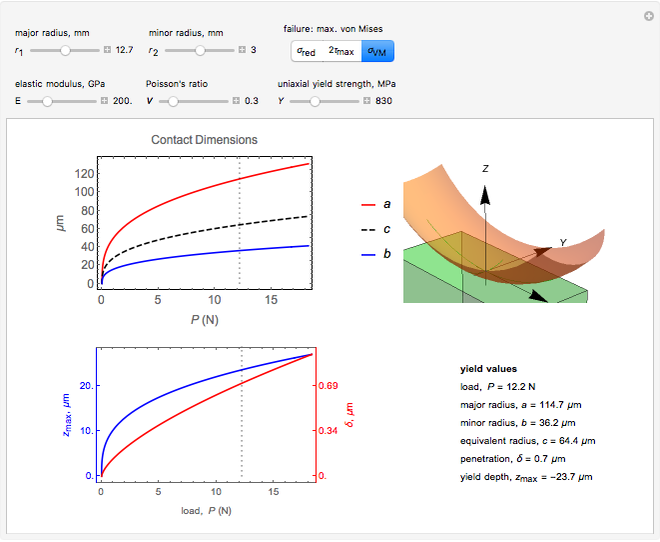
This Demonstration codes this formulation allowing you to see the relative dimensions of the indenter and the contact ellipse when zooming in. It also reports the values at yield for given material properties  ,
,  and
and  for the criterion chosen.
for the criterion chosen.
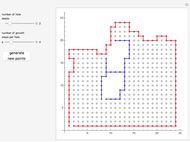
Two plots are shown to the left. Top shows the variation in contact dimensions  ,
,  and
and  with increasing load
with increasing load  .
.
The bottom shows the variation in penetration  (red curve, right
(red curve, right  axis) and position
axis) and position  (blue curve, left
(blue curve, left  axis) with load
axis) with load  . Dotted lines plot the position at yield for the criterion chosen.
. Dotted lines plot the position at yield for the criterion chosen.
A key fact is that  is very sensitive to
is very sensitive to  and
and  . The earlier equation can be rewritten as
. The earlier equation can be rewritten as
 .
.
The equation above has two roots; one of which is  for any
for any  . This is the correct root to use when
. This is the correct root to use when  or
or  .
.
References
[1] K. L. Johnson, Contact Mechanics, 1st ed., Cambridge: Cambridge University Press, 1985.
[2] H. R. Thomas and V. A. Hoersch, Stress Due to the Pressure of One Elastic Solid upon Another, Bulletin No. 212, Engineering Experimental Station, University of Illinois, 1930.
Permanent Citation