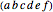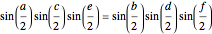Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Concurrent Diagonals in a 30-Gon

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

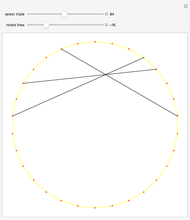
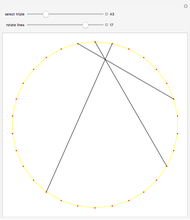
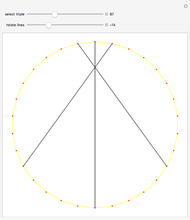
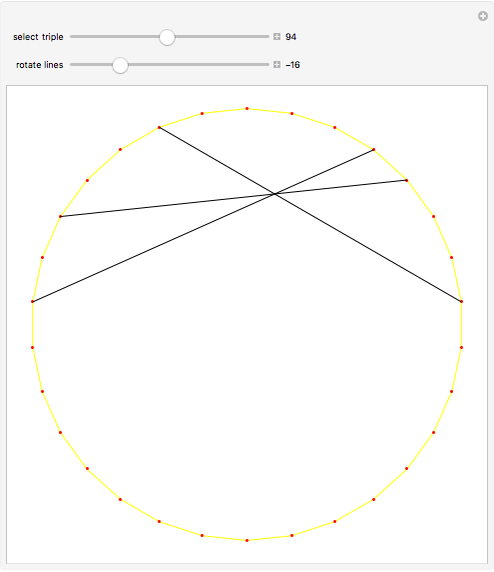
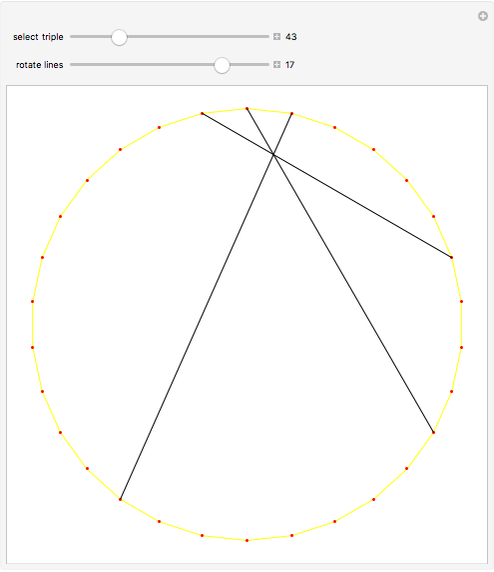
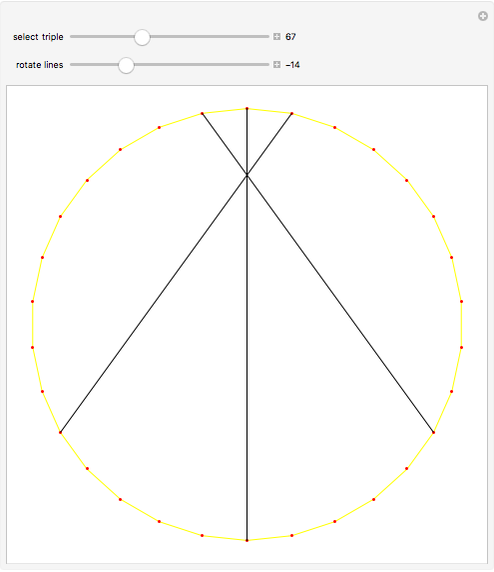
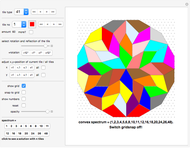
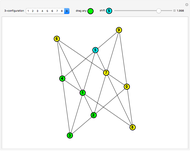
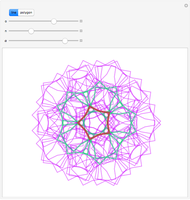
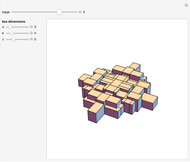
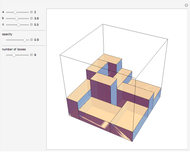
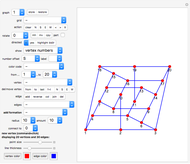
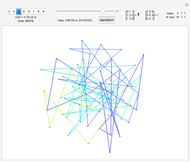
When three lines meet at a point, they are concurrent. For the diagonals of a 30-gon, out of the 16801 intersection points, there are 3001 points where three or more lines intersect, with 193 different ways to select three concurrent diagonals.

[more]

Consider six points that divide a circle into arcs . If , then the three lines connecting opposing points are concurrent [1]. This property was used to find the sets of lines. By the pizza theorem, half the circle is covered by wedges , and half by wedges .

[less]

Contributed by: Ed Pegg Jr (November 2015)
Open content licensed under CC BY-NC-SA

Snapshots

Details

In the initialization, {1,3,9,4,8,5,14} is a sample dataset (selected triple 102). The first six numbers are a partition of 30; the last number is the sector of the 30-gon where the intersection occurs.

References

[1] B. Poonen and M. Rubinstein, "The Number of Intersection Points Made by the Diagonals of a Regular Polygon," arxiv.org/abs/math/9508209.

[2] Wikipedia. "Pizza Theorem." (Nov 13, 2015) en.wikipedia.org/wiki/Pizza_theorem.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send