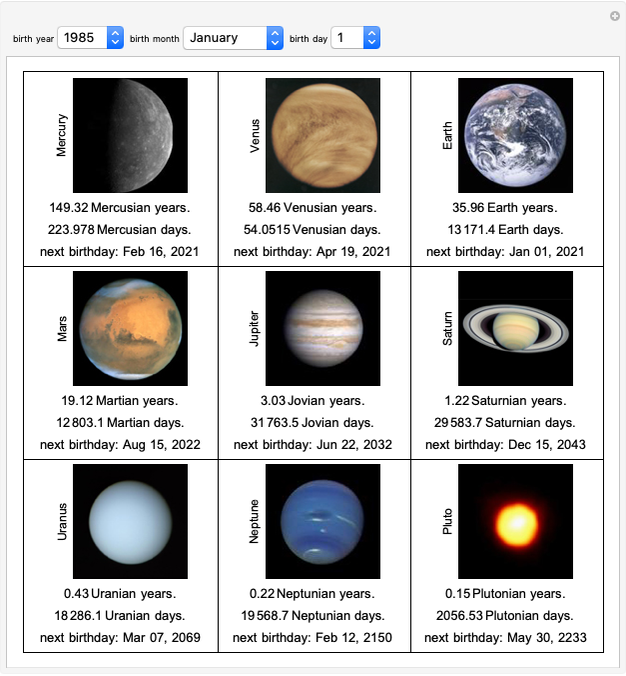
Power of a Test about a Binomial Parameter

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
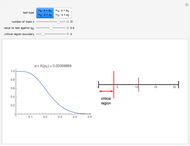
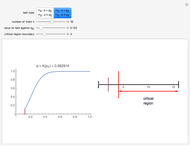
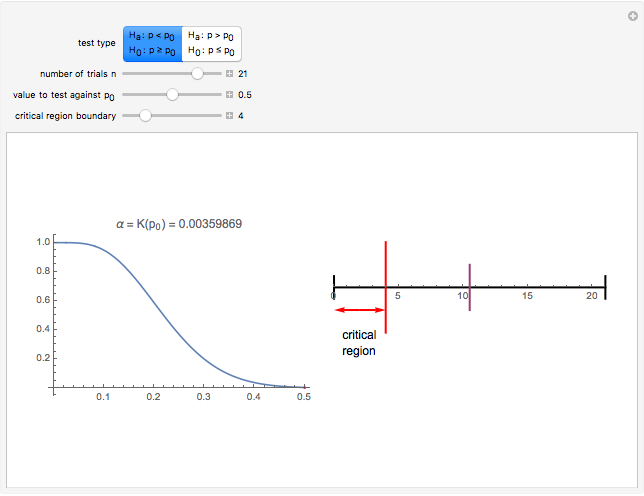
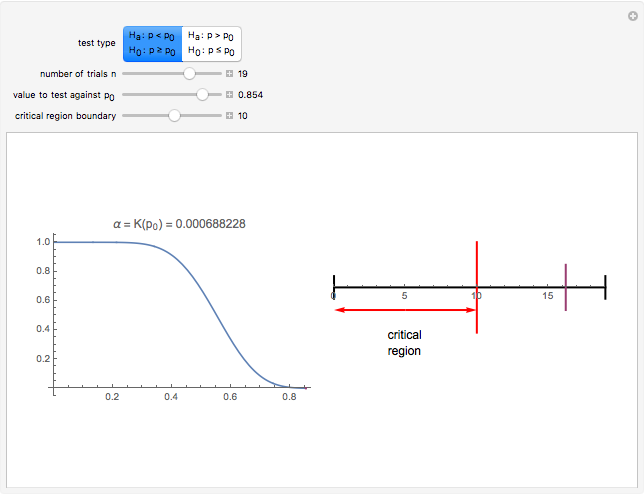
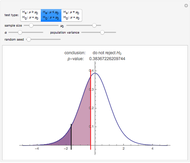
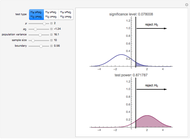
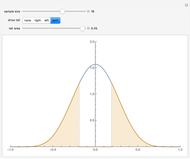
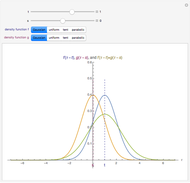
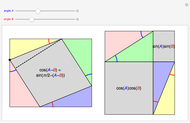
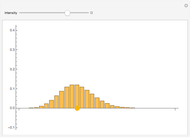
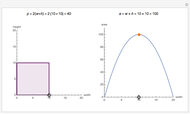
The left plot shows the power function of the selected test with the value of 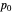 marked in purple. The power function is a function of the true value of the parameter
marked in purple. The power function is a function of the true value of the parameter 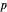 . Its value at
. Its value at 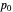 is called the significance of the test. The right image shows the critical region as a subset of the range of the test statistic. The expected value of the test statistic if
is called the significance of the test. The right image shows the critical region as a subset of the range of the test statistic. The expected value of the test statistic if 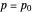 ,
, 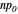 is marked in purple.
is marked in purple.
Contributed by: Chris Boucher (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
To test the hypothesis 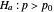 or the hypothesis
or the hypothesis 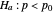 about a Bernoulli parameter
about a Bernoulli parameter  , it is decided that if the number of successes in
, it is decided that if the number of successes in 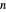 independent trials is above (for the first test) or below (for the second test) a certain threshold, then the hypothesis will be accepted. This threshold is the boundary of what is called the critical region—whether the number of successes falls in this region determines the outcome of the test. The probability that the number of successes falls in the critical region is a function of the true value of
independent trials is above (for the first test) or below (for the second test) a certain threshold, then the hypothesis will be accepted. This threshold is the boundary of what is called the critical region—whether the number of successes falls in this region determines the outcome of the test. The probability that the number of successes falls in the critical region is a function of the true value of 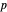 . In the case of the test
. In the case of the test 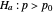 , the power function gives this probability for
, the power function gives this probability for 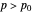 . If
. If  the number of successes falls outside the critical region, then a type II error (false negative) occurs. The power function gives the opposite of this probability, that is, for each value of
the number of successes falls outside the critical region, then a type II error (false negative) occurs. The power function gives the opposite of this probability, that is, for each value of 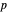 covered by
covered by 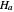 , the power function gives the probability that the test does not yield a false negative.
, the power function gives the probability that the test does not yield a false negative.
Permanent Citation