Convex Hull and Delaunay Triangulation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
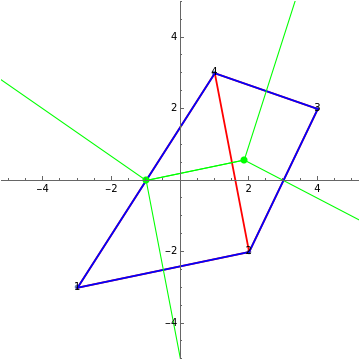
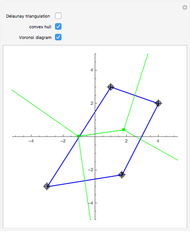
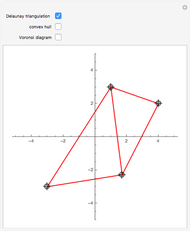
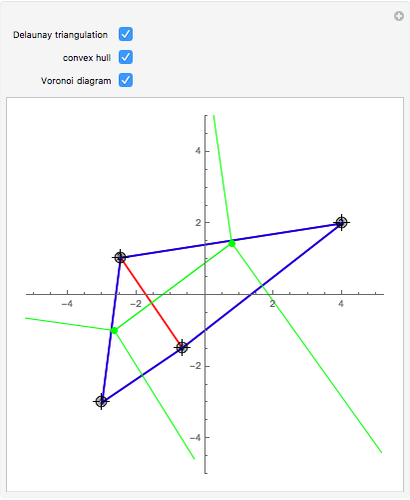
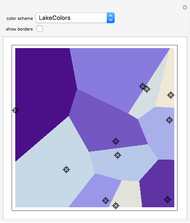
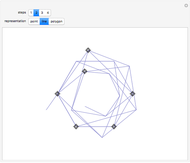
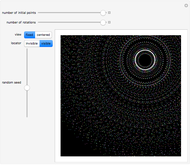
For three or more points, you can see the convex hull (blue), the Delaunay triangulation (red), or the Voronoi diagram (green).
Contributed by: Marko Petkovic (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The convex hull of a given set  is the smallest convex set that contains
is the smallest convex set that contains  . If
. If  is finite, that is, if
is finite, that is, if  , where the
, where the  are points, then the convex hull is always a polygon whose vertices are a subset of
are points, then the convex hull is always a polygon whose vertices are a subset of  .
.
The Delaunay triangulation of a given set of points  is a triangulation of the convex hull of
is a triangulation of the convex hull of  such that no point of
such that no point of  is inside the circumcircle of any triangle of
is inside the circumcircle of any triangle of  .
.
The Voronoi diagram of the set of points  is the plane partition containing the regions
is the plane partition containing the regions  of points whose distance from
of points whose distance from  is no greater than the distance from any other point
is no greater than the distance from any other point  . In the graph theory sense, the Voronoi diagram is the dual graph of the Delaunay triangulation.
. In the graph theory sense, the Voronoi diagram is the dual graph of the Delaunay triangulation.
Permanent Citation