Current-Carrying Coil in an External Magnetic Field

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
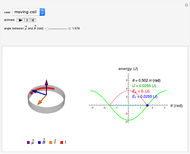
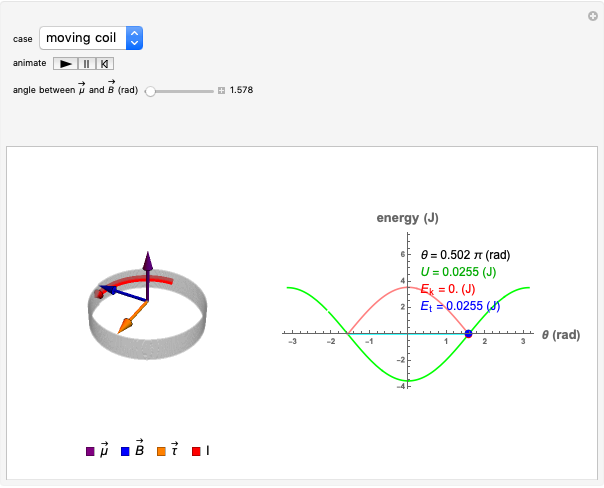
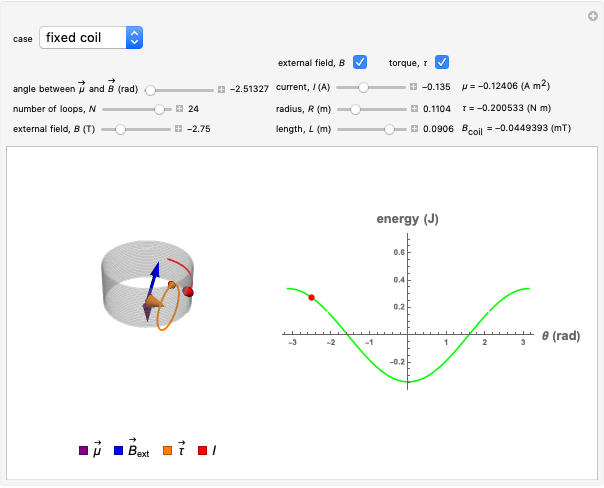
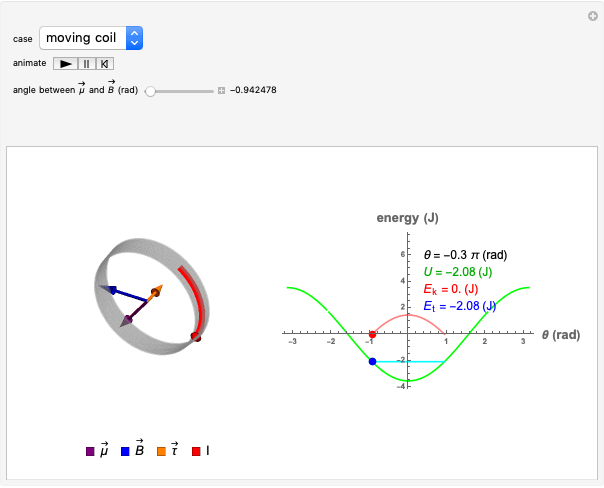
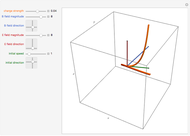
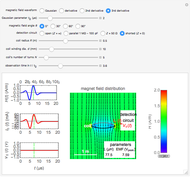
This Demonstration shows the motion of a current-carrying coil placed in an external magnetic field. The coil behaves as a magnetic dipole and so experiences a torque in the presence of an external magnetic field. We consider two scenarios.
[more]
Contributed by: Fis. Fernando Moncada and Telmo Aguilar (June 2021)
Suggested by: Esteban Irribarra
(Developed in the Physics Laboratory of Escuela Politécnica Nacional)
Open content licensed under CC BY-NC-SA
Snapshots
Details
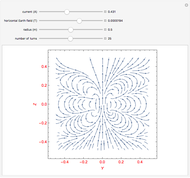
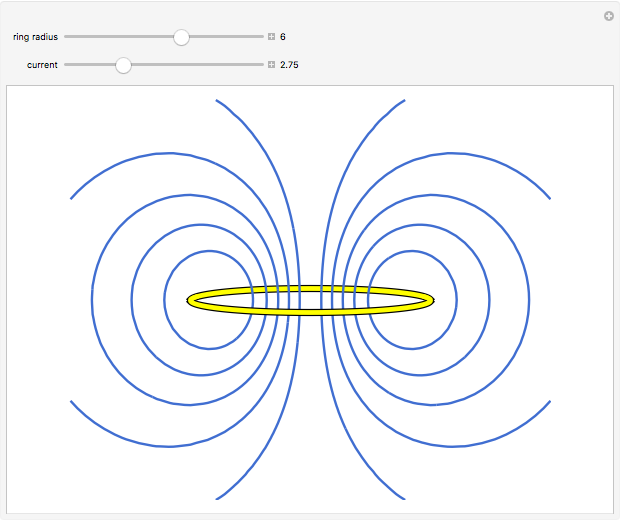
The magnetic field 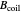 produced by a large current-carrying coil is obtained by Ampere's law. Inside the coil it is given by:
produced by a large current-carrying coil is obtained by Ampere's law. Inside the coil it is given by:
 ,
,
where
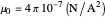 is the vacuum magnetic permeability,
is the vacuum magnetic permeability,
 is the density of loops,
is the density of loops,
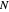 is the total number of loops,
is the total number of loops,
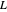 is the length of the coil and
is the length of the coil and
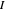 is the magnitude of its current.
is the magnitude of its current.
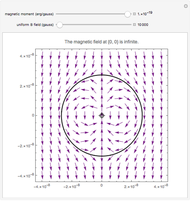
A loop that carries a magnetic field has a magnetic dipole moment. A small coil of 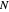 loops has the approximate magnetic dipole moment
loops has the approximate magnetic dipole moment  given by:
given by:
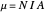 ,
,
where 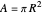 is the area of the loop and
is the area of the loop and 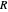 is its radius. The magnetic dipole moment is a vector and its direction is given by the right-hand rule according to the direction in which the current is flowing. If the current is counterclockwise, the dipole moment is directed upward, and if the current is clockwise, the dipole moment is directed downward.
is its radius. The magnetic dipole moment is a vector and its direction is given by the right-hand rule according to the direction in which the current is flowing. If the current is counterclockwise, the dipole moment is directed upward, and if the current is clockwise, the dipole moment is directed downward.
A magnetic dipole moment 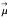 in the presence of an external magnetic field
in the presence of an external magnetic field experiences a torque
experiences a torque 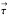 given by
given by
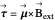 .
.
A magnetic dipole also stores energy in the presence of an external field. Its potential energy  is given by
is given by
 .
.
A dipole in an external field experiences a torque that makes it rotate. When it rotates, it transforms part of its potential energy into kinetic energy 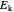 maintaining its total energy
maintaining its total energy 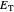 constant, according to the conservation of energy law:
constant, according to the conservation of energy law:
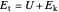 .
.
Permanent Citation