Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Magnetic Field of a Current Loop

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

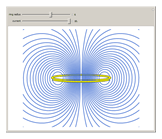
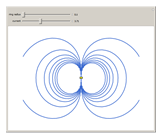
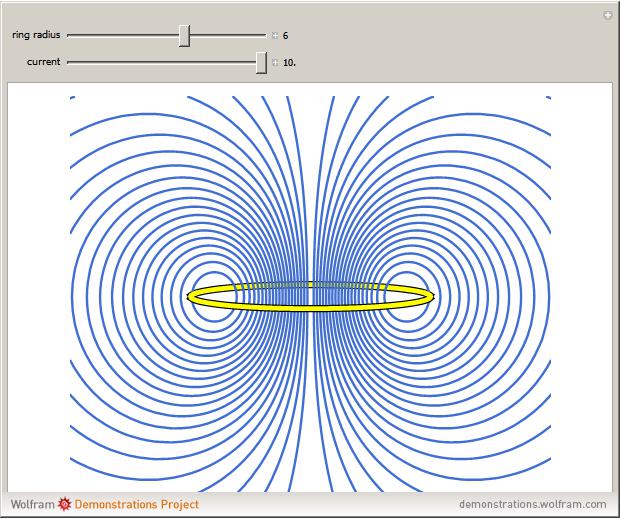
A electrical current moving around a circular loop of radius , shown in yellow from a lateral point of view, produces a magnetic field, with lines of force shown as blue loops. For clarity, only lines of force in the vertical plane bisecting the ring () are shown.

[more]

The strength of the magnetic field is indicated by the density of the lines of force. The magnitude is expressed in units of . The field is cylindrically symmetrical about the axis of the ring. By a right-hand rule, a counterclockwise current produces magnetic lines of force that point upward inside the ring, downward outside the ring. At distances , the ring behaves like a magnetic dipole , with vector potential . As (with constant), this approaches the field of a point magnetic dipole.

It is shown in the Details section that a contour plot of the vector potential in the plane coincides with the magnetic lines of force.

[less]

Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The vector potential for a ring of current can be solved exactly in terms of complete elliptic integrals. Transforming to Cartesian coordinates in the vertical plane bisecting the ring, the following approximation is found to be indistinguishable graphically from the exact solution: . The magnetic induction is given by , so that and . Since this is a magnetostatic problem, the magnetic induction can also be represented in terms of a scalar potential , so , . The magnetic lines of force are represented by contours orthogonal to those of the potential , thus . This equation can be satisfied by

Reference: J. D. Jackson, Classical Electrodynamics, 3rd ed., New York: John Wiley & Sons, 1999 pp. 181–186.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send