Motion of Three Magnetic Vortices

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
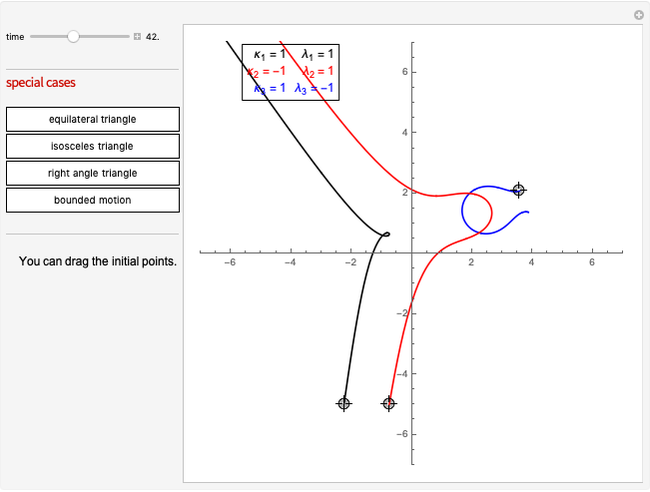
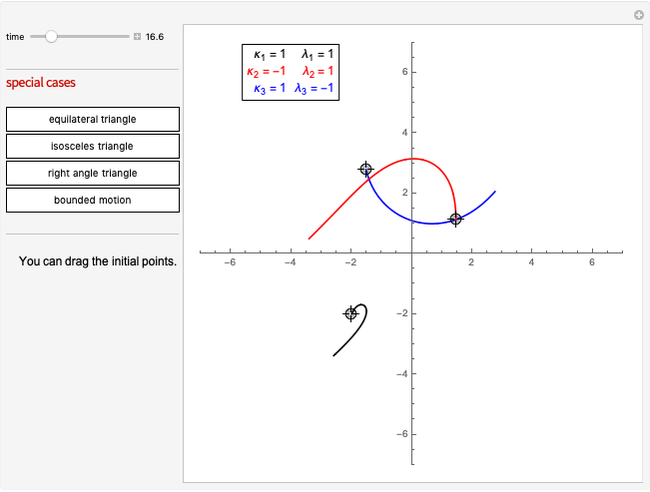
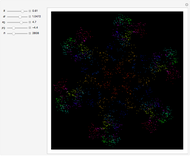
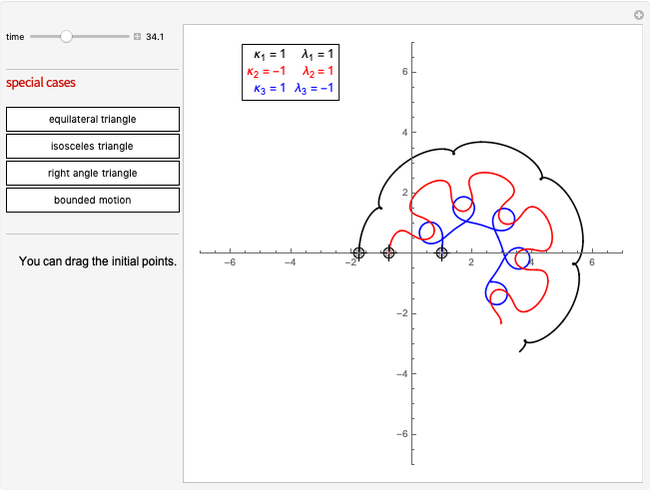
This Demonstration shows a simulation of the dynamics of three point-like magnetic vortices in a magnetic film. Their dynamics are similar to that of ordinary vortices, but one additional parameter occurs. Based on the analysis of the dynamical equations, four special cases that illustrate the general behavior of vortex dynamics are considered.
Contributed by: Menelaos Ampartzakis, Dimitris Karamanidis, Dimitris Papasotiriou and Giannis Sofras (May 2019)
Supervised by: Stavros Komineas
Developed in the context of a course on Mathematical Modelling and Simulation at the University of Crete.
Open content licensed under CC BY-NC-SA
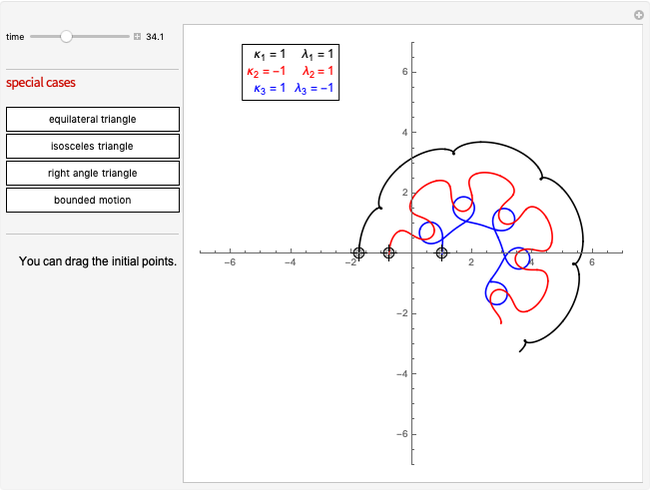
Snapshots
Details
Simulation of the dynamics of three point-like magnetic vortices in a magnetic film is considered. These are vortices of magnetization in a magnetic material, with sizes ranging from 10 to 50 nanometers. They are mathematically similar to ordinary vortices in fluids.
The equations of motion for the vortex positions are given in [1, Eq. (4)]. They are a generalization of the Helmholtz–Kirchhoff equations for point vortices in ordinary fluids. The equations of motion describe a Hamiltonian system that is completely integrable; that is, all vortex trajectories can be formally found by integration based on the conserved quantities of energy, linear momentum and angular momentum. A complete solution for three fluid vortices was given in the 1877 dissertation of Gröbli [2], reviewed in [3]. A complete study for the system of magnetic vortices is given in [1].
Each vortex is characterized by two integers:  is the vortex number (
is the vortex number ( , or
, or  for vortices and antivortices, respectively), and
for vortices and antivortices, respectively), and  specifies the direction of the magnetic vortex (
specifies the direction of the magnetic vortex ( or
or  for magnetization pointing up or down, respectively), which does not pertain in the case of ordinary vortices. We focus on the cases of vortices with parameters
for magnetization pointing up or down, respectively), which does not pertain in the case of ordinary vortices. We focus on the cases of vortices with parameters  ,
,  ,
, 
 These cannot be realized in ordinary fluids, but only for magnetic vortices (see cases 2 through 4 following).
These cannot be realized in ordinary fluids, but only for magnetic vortices (see cases 2 through 4 following).
We consider four special cases:
1. Three identical vortices forming an equilateral triangle, rotating around the center.
2. A vortex-antivortex pair colliding on a third vortex, scattering at an angle while the third vortex merely changes its position.
In this case a transmutation of linear momentum into position occurs; that is, a vortex-antivortex pair changes its motion while another vortex changes its position in such a way that the conservation law for momentum/position remains satisfied.
3. Three vortices collide at a common point in finite time, thus creating a singularity in the solution.
4. Three vortices are confined in motions bounded in space.
References
[1] S. Komineas and N. Papanicolaou, "Gro¨bli Solution for Three Magnetic Vortices," Journal of Mathematical Physics, 51, 2010 042705. doi:10.1063/1.3393506.
[2] W. Gröbli, Spezielle Probleme über die Bewegung geradliniger paralleler Wirbelfäden, Zürich: Zürcher and Furrer, 1877. Reprinted in Vierteljahrsschrift der Natforschenden Gesellschaft Zurich, 22, 1877 p. 37–81; 22, 1877 p. 129–165.
[3] H. Aref, N. Rott and H. Thomann, "Gro¨bli's Solution of the Three-Vortex Problem," Annual Review of Fluid Mechanics, 24(1), 1992 pp. 1–21. doi:10.1146/annurev.fl.24.010192.000245.
Permanent Citation