Definition and Equations of an Ellipse

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
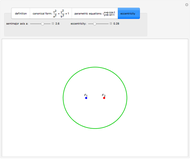
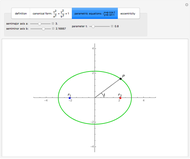
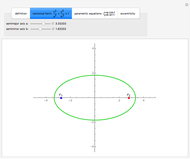
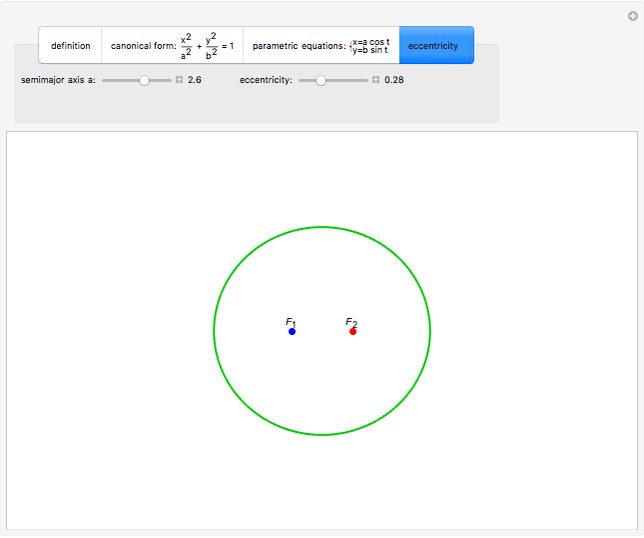
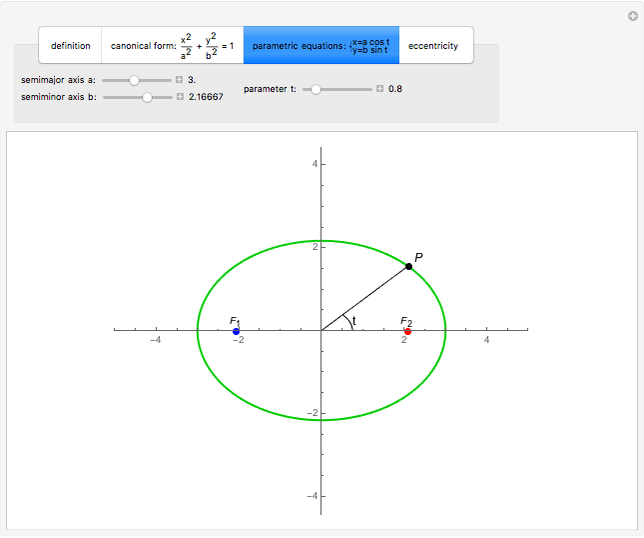
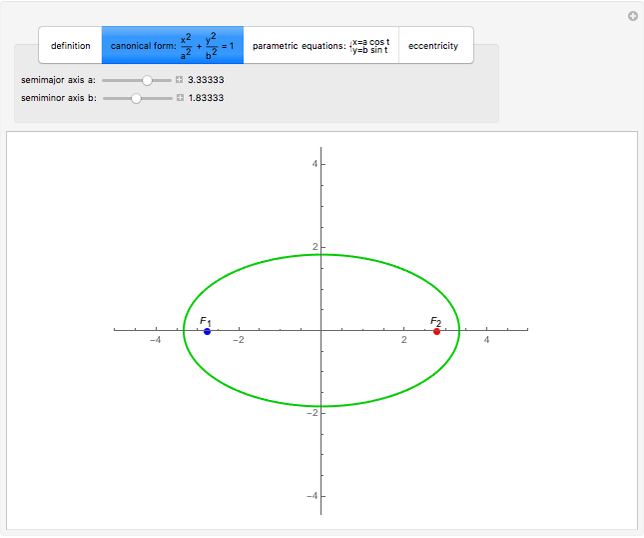
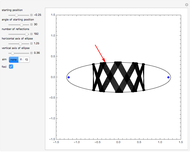
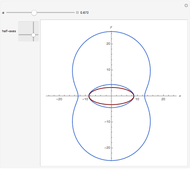
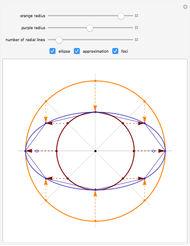
This Demonstration illustrates the definition of an ellipse, the canonical and parametric equations of the ellipse, and the effect of eccentricity on the shape of an ellipse.
Contributed by: V. Tomilenko (June 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
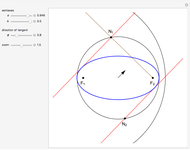
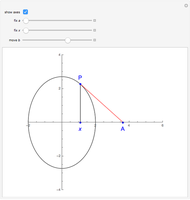
Given two points,  and
and  (the foci), an ellipse is the locus of points
(the foci), an ellipse is the locus of points  such that the sum of the distances from
such that the sum of the distances from  to
to  and
and  is a constant.
is a constant.
To get equations, choose a Cartesian coordinate system as follows:
1. the  axis is directed along the line passing through the foci
axis is directed along the line passing through the foci  and
and  ;
2. the origin is taken to be the midpoint of the segment
;
2. the origin is taken to be the midpoint of the segment  ;
3. the foci
;
3. the foci  and
and  are separated by a distance
are separated by a distance  .
.
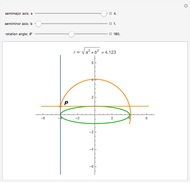
If the sum of the distances from a point  on an ellipse to the two foci is
on an ellipse to the two foci is  , then
, then  and
and  are the major and minor semiaxes of the ellipse.
are the major and minor semiaxes of the ellipse.
Permanent Citation