Detachment and Tendency of a Single Variable Function

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
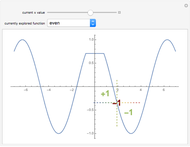
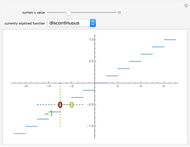
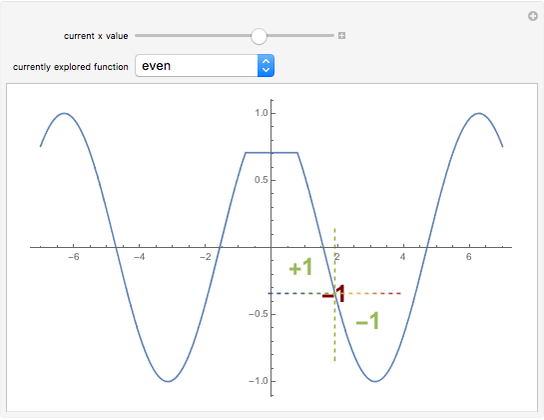
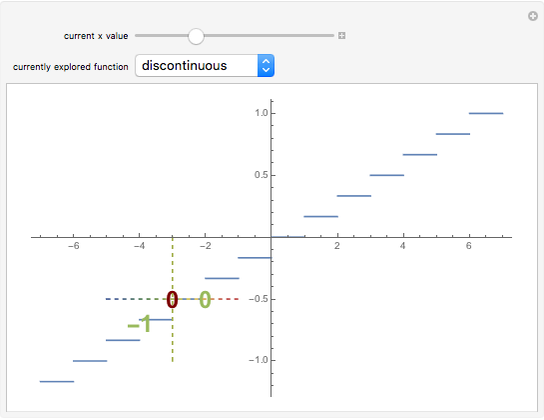
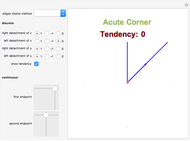
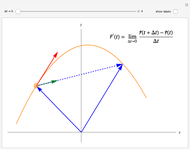
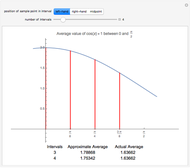
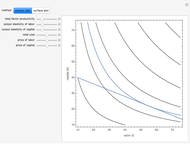
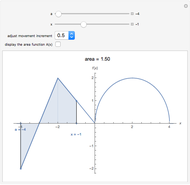
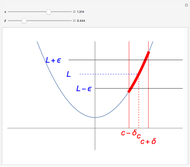
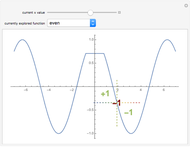
Depicted are the pointwise operators: "detachment from left or right" and "tendency" applied to a given function. In the suggested graphs, the value of the one-sided detachments is colored in green, and the value of the tendency is colored in red.
[more]
Contributed by: Amir Finkelstein (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Ever since the early 1980s, computer scientists have been using discrete versions of Green's and Stokes's theorems, also known as the "summed area tables" algorithms. These theorems were shown to provide a tremendous computational gain, since they fit precisely to the needs of discrete geometry researchers due to their discrete nature. It was suggested that these theorems are actually derived from a differently defined calculus, namely the "calculus of detachment". The main operator of this theory is defined by a mixture of the discrete and continuous to form a semi-discrete version of the familiar derivative. This approach to analyze functions is hence more suitable for computers (in order to save computation time), and the simplicity of the definition allows further research in other areas of classical analysis. A basic and not very comprehensive video introduction to this theory is available, and a preprint is also available.

Permanent Citation
"Detachment and Tendency of a Single Variable Function"
http://demonstrations.wolfram.com/DetachmentAndTendencyOfASingleVariableFunction/
Wolfram Demonstrations Project
Published: March 7 2011