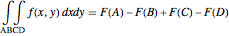Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Double Integrals by Summing Values of a Cumulative Distribution Function

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

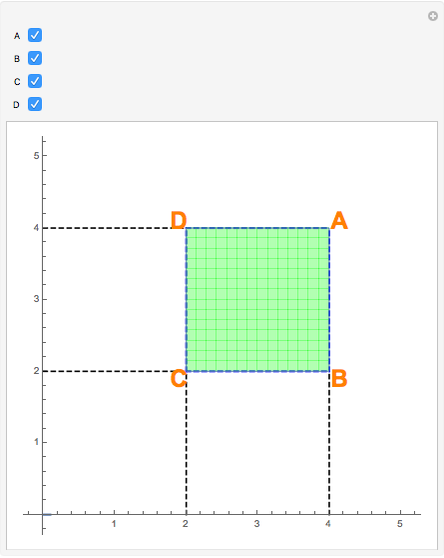
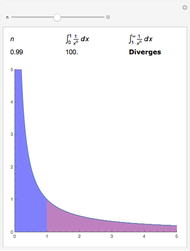
Let 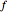be a function, and suppose that its "cumulative distribution function" 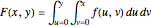, is known. 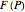is the integral of 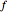over the rectangle below and to the left of 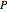, and the double integral of 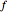over a rectangle can be computed easily in terms of the values of 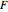at the corners via:

[more]

.

Checking boxes causes a region to be shaded such that the combination values at the checked corners is the integral of over the shaded region.

[less]

Contributed by: Amir Finkelstein (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

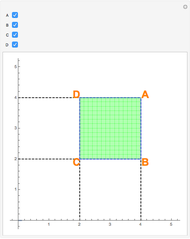
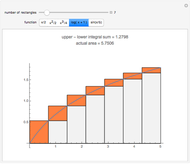
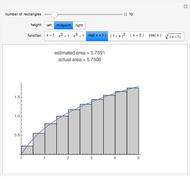
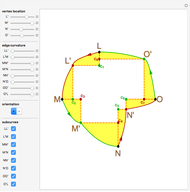
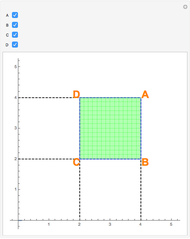
Snapshot 1: only the vertex 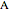is chosen in the linear combination

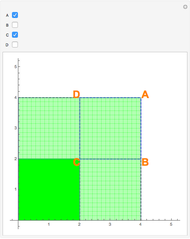
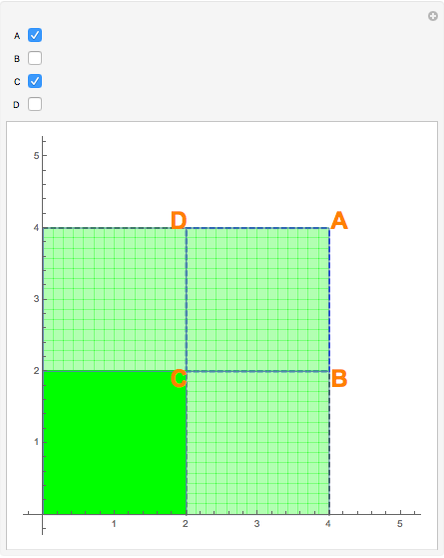
Snapshot 2: both vertices 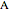and 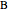are chosen in the linear combination; light green regions are where the function's double integral was added only once in the linear combination with a positive coefficient; dark green regions are where the function's double integral was added twice in the linear combination

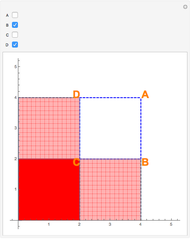
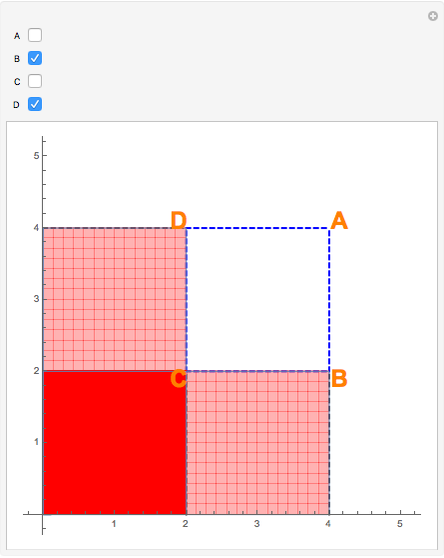
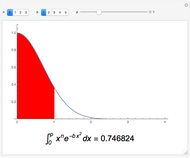
Snapshot 3: Both vertices C and D are chosen in the linear combination; light red regions are where the function's double integral was subtracted only once in the linear combination; dark green regions are where the function's double integral was subtracted twice in the linear combination

More information regarding this algorithm is available in Wikipedia,and in the following papers:

[1] F. C. Crow, "Summed-Area Tables for Texture Mapping," in SIGGRAPH '84: Proceedings of the 11th Annual Conference on Computer Graphics and Interactive Techniques, 1984 pp. 207–212.

[2] P. Viola and M. Jones, "Robust Real-Time Object Detection," International Journal of Computer Vision, 57(2), 2002 pp. 137–154. http:\\research.microsoft.com/en-us/um/people/viola/pubs/detect/violajones_ijcv.pdf

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send