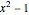Limit of a Function at a Point
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
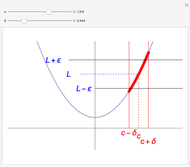
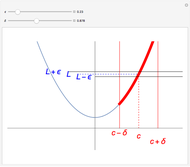
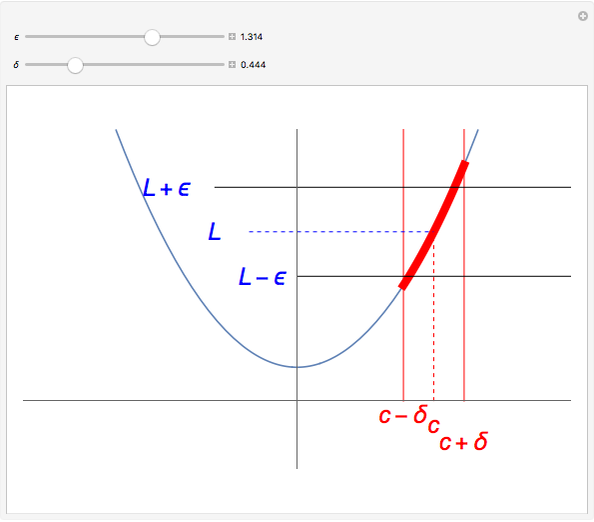
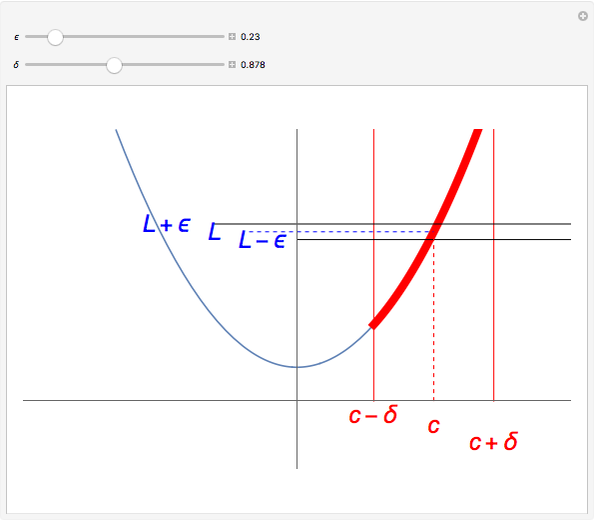
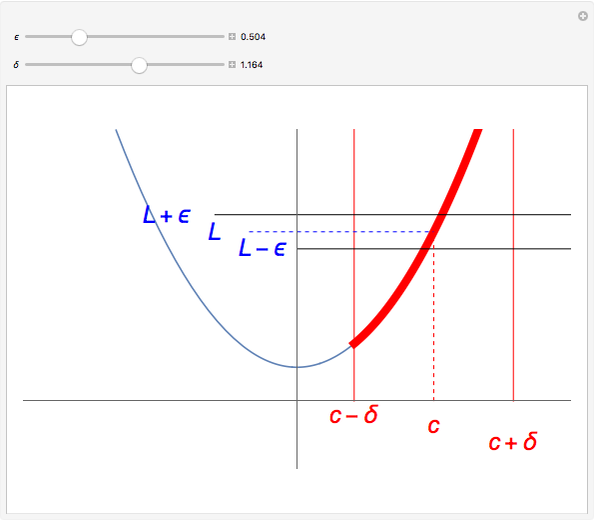
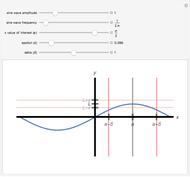
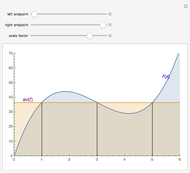
A function assigns a value 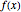 given any point
given any point  . We say that a function
. We say that a function 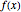 has a limit
has a limit 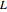 at a point
at a point  if
if 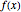 gets closer and closer to
gets closer and closer to 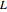 as
as  moves closer and closer to
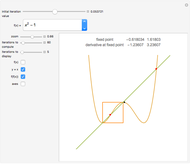
moves closer and closer to  . A more formal definition of
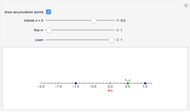
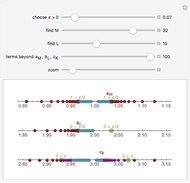
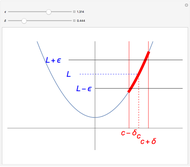
. A more formal definition of 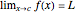 is: for each
is: for each 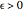 , there exists a
, there exists a 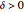 such that
such that 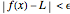 whenever
whenever 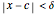 . Note that
. Note that  depends on
depends on  : "You give me an
: "You give me an  and I'll find you a
and I'll find you a  ".
".
Contributed by: Quinn Morris (September 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation