Deterministic versus Stochastic Chemical Kinetics

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
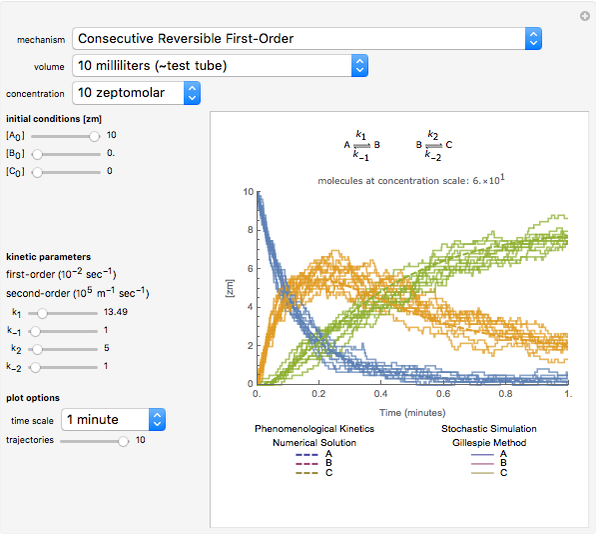
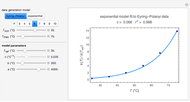
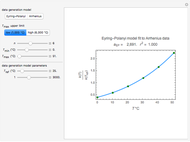
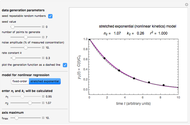
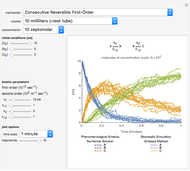
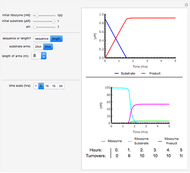
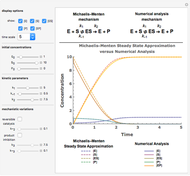
Traditional phenomenological kinetics uses first-order ordinary differential equations (ODEs) to describe the rate of change of the species in a chemical reaction. The solution to these equations provides expressions for the concentration of each species as a function of time. The use of ODEs to describe rate laws implies that concentrations are continuous quantities. As a consequence, this model is deterministic and provides exact solutions with no uncertainty involved. Because Avogadro's number is so enormous  , even a nanomole of material involves over 100 trillion molecules, so in a typical lab-scale reaction it is reasonable to assume that concentrations are continuous variables. However, when concentrations or volumes become tiny (as in the inside of a human cell), this assumption can break down.
, even a nanomole of material involves over 100 trillion molecules, so in a typical lab-scale reaction it is reasonable to assume that concentrations are continuous variables. However, when concentrations or volumes become tiny (as in the inside of a human cell), this assumption can break down.
Contributed by: Brian M. Frezza (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
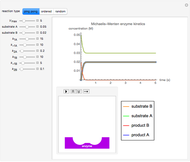
The Gillespie method simulates each reaction step on a molecular level [1]. Although it is more realistic physically, it is computationally more demanding. As the number of molecules increases, the stochastic results will converge to the deterministic solutions. Therefore the model will neglect trajectories for any reactions involving more then 1,000 molecules and will halt any simulation after 5,000 steps so as to keep runtime reasonable for dynamic interactivity.
The author of this Demonstration is a doctoral candidate at The Scripps Research Institute in La Jolla, CA, with thesis adviser M. Reza Ghadiri.
[1] D. T. Gillespie, "Exact Stochastic Simulation of Coupled Chemical Reactions," The Journal of Physical Chemistry, 81(25), 1977 pp. 2340-2361.
Permanent Citation
"Deterministic versus Stochastic Chemical Kinetics"
http://demonstrations.wolfram.com/DeterministicVersusStochasticChemicalKinetics/
Wolfram Demonstrations Project
Published: March 7 2011