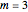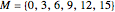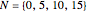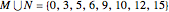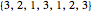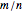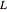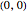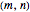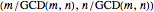Differences of the Union of Two Arithmetic Progressions and Christoffel Paths

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Let  and
and  be two positive integers with
be two positive integers with  . Define
. Define  and
and 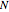 to be the arithmetic progressions
to be the arithmetic progressions 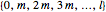 and
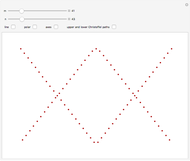
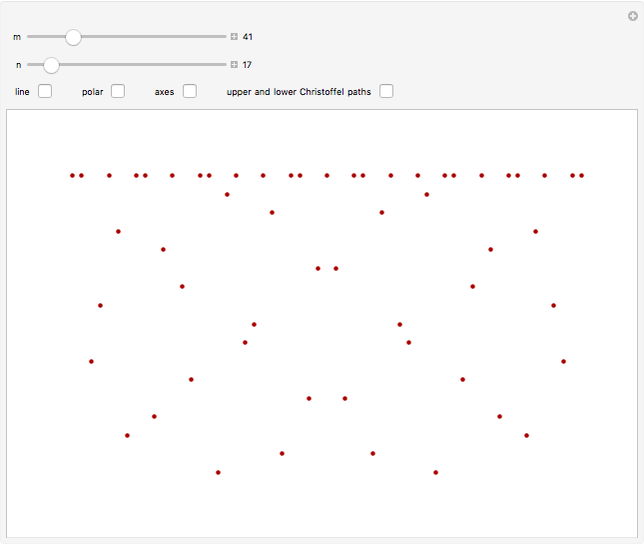
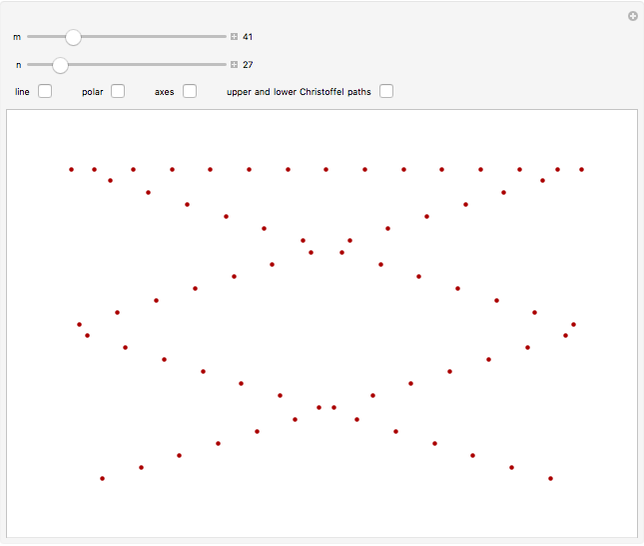
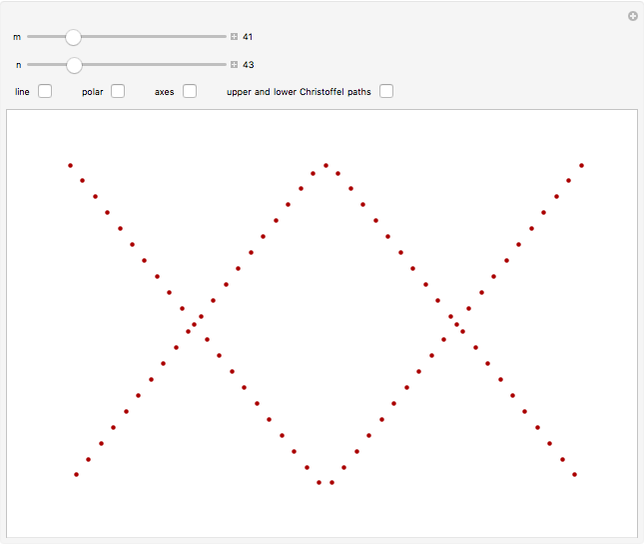
and 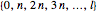 . The set
. The set 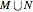 partitions the interval
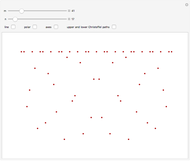
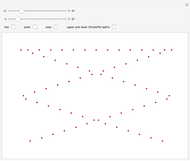
partitions the interval 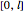 into subintervals, whose lengths are plotted here. The plots are periodic, so it makes sense to wrap them around a circle with a polar plot.
into subintervals, whose lengths are plotted here. The plots are periodic, so it makes sense to wrap them around a circle with a polar plot.
Contributed by: George Beck (August 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] Wikipedia. "Beat (Acoustics)." (Aug 3, 2015) en.wikipedia.org/wiki/Beat_%28 acoustics %29.
[2] J. Berstel, A. Lauve, C. Reutenauer, and F. Saliola, Combinatorics on Words: Christoffel Words and Repetitions in Words, 2008, p. 54.
Permanent Citation