Duffing Oscillator

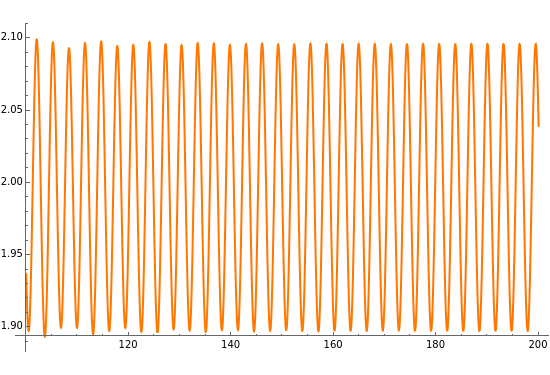
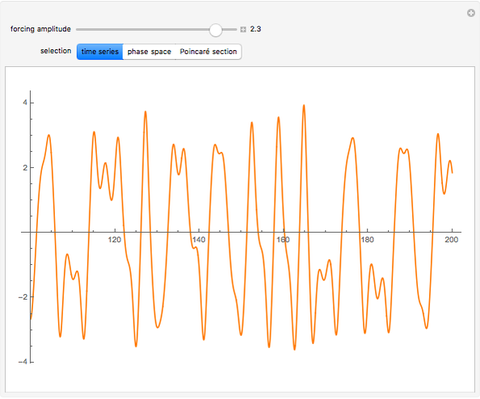
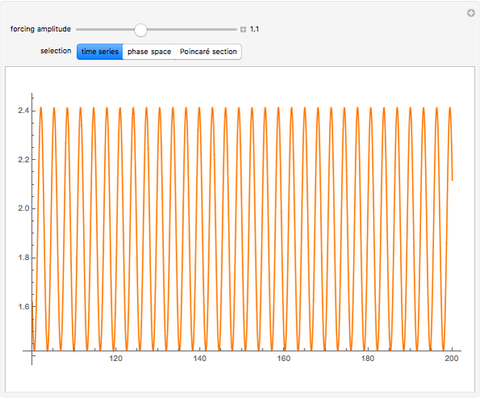
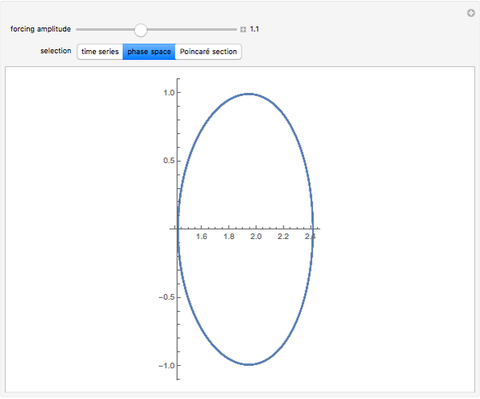
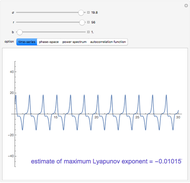
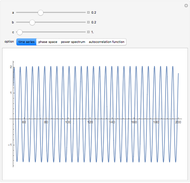
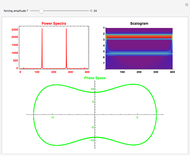
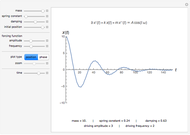
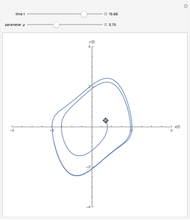
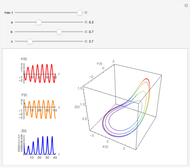
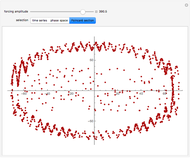
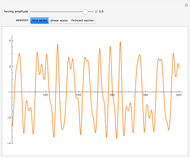
The Duffing oscillator moves in a double well potential, sometimes characterized as nonlinear elasticity, with sinusoidal external forcing. It is described by the equation . We consider the parameters , , , , , and . Solutions to the oscillator equation can exhibit extreme nonlinear dynamics, including limit cycles, strange attractors, and chaotic behavior. The system is, as expected, highly sensitive to the initial conditions.

When the periodic force () that drives the system is large, the motion can become chaotic and the phase space diagram can develop a strange attractor. A Poincaré section can be plotted by taking one phase space point in each period of the driving force. In the simplest cases, when the system enters a limit cycle, the Poincaré section reduces to a single point. A strange attractor is usually associated with a complicated fractal curve.