Effect of Temperature on Partial Miscibility in a Binary-Liquid System

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
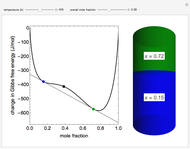
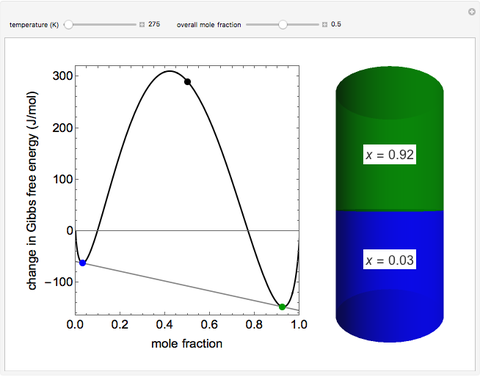
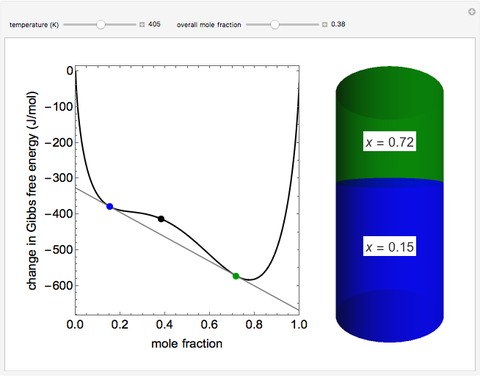
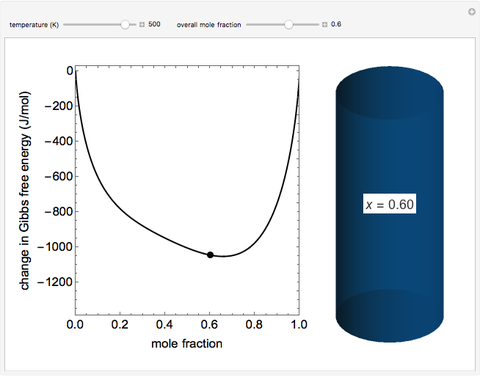
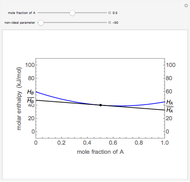
This Demonstration plots the change in Gibbs free energy versus mole fraction of one component in a non-ideal binary mixture. Two liquid phases form when the Gibbs free energy is lower for the two phases than for one phase. A line that is tangent to the Gibbs free energy curve at two points (blue and green points) represents the Gibbs free energy change over the mole fraction range between the two points. The mole fractions at the blue and green points are the mole fractions of the two phases, and these mole fractions are shown on the container on the right. The size of each phase on the right is proportional to the amount of that phase, and these amounts are obtained from a mass balance (lever rule). Increasing the temperature with the slider decreases the range of partial miscibility. The slider on the right changes the overall mole fraction, and the black circle represents that mole fraction.
Contributed by: Kaiyuan Tang (December 2017)
Additional contributions by: Rachael L. Baumann and John L. Falconer
Department of Chemical and Biological Engineering, University of Colorado Boulder
Open content licensed under CC BY-NC-SA
Snapshots
Details
For the non-ideal mixture modeled in this simulation, the change in Gibbs free energy when two components are mixed (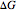 in units of J/mol) is:
in units of J/mol) is:
 ,
,
where  is the mole fraction of one component in a binary mixture (
is the mole fraction of one component in a binary mixture ( is the mole fraction of the second component),
is the mole fraction of the second component),  and
and  are constants,
are constants,  is the gas constant (J/[mol K]), and
is the gas constant (J/[mol K]), and  is temperature (K).
is temperature (K).
The Gibbs free energy of mixing for an ideal solution is composed of two parts:
The empirical term that models non-ideal behavior is the excess Gibbs free energy:
 .
.
For this system, the mixture separates into two liquid phases over some range of composition; each phase contains both components. Phase separation occurs if the two phases have a lower Gibbs free energy than a single phase. This means if a linear combination of the Gibbs free energies of the two phases (determined in the graph by a line tangent to the curve at two points) is lower than the Gibbs free energy of the mixture, then phase separation occurs. As the temperature increases, the range of compositions where phase separation occurs decreases. Mathematically, the two points where the tangent line intersects the curve are the mole fractions where the derivative of  with respect to
with respect to  is same.
is same.
References
[1] S. R. Logan, “The Behavior of a Pair of Partially Miscible Liquids,” Journal of Chemical Education, 75(3), 1998 p. 339. doi:10.1021/ed075p339.
[2] J. P. Erikson, “Partially Miscible Water-Triethylamine Solutions and Their Temperature Dependence,” Journal of Chemical Education, 94(1), 2017 pp. 75–78. doi:10.1021/acs.jchemed.6b00489.
Permanent Citation