Material and Energy Balances in a Reactor with Heat Exchange

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
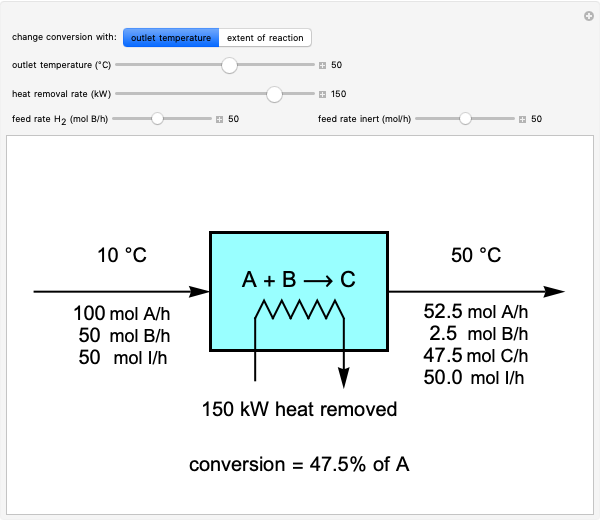
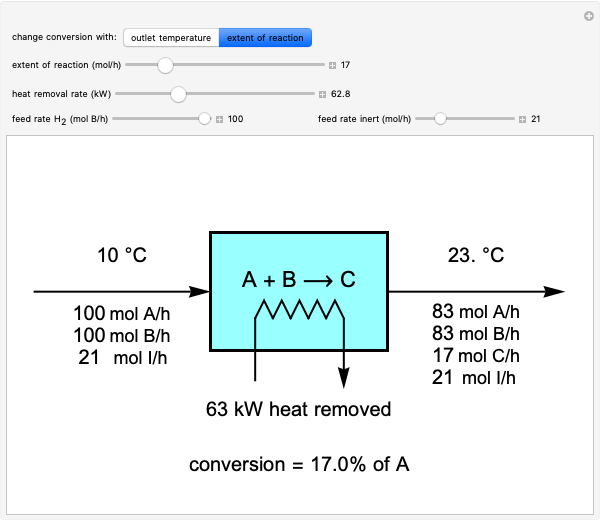
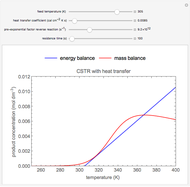
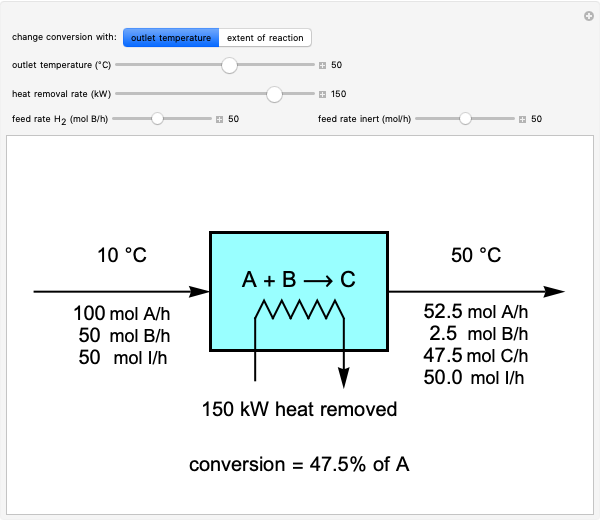
This Demonstration calculates material and energy balances for a reactor with heat transfer. The reaction  is acetylene (
is acetylene ( ) hydrogenation to ethylene (
) hydrogenation to ethylene ( ), where
), where  is hydrogen. The feed rate of
is hydrogen. The feed rate of  is fixed at 100 mol/h; use sliders to change the feed rates of
is fixed at 100 mol/h; use sliders to change the feed rates of  and an inert (
and an inert ( ). Use either the extent of reaction or the outlet temperature to change the conversion of
). Use either the extent of reaction or the outlet temperature to change the conversion of  . Select "extent of reaction" to set the extent of reaction and heat removal rate with sliders to change the outlet temperature. Select "outlet temperature" to change the outlet temperature and heat removal rate to determine the conversion, and the heat removed is fixed to the value that results in the selected outlet temperature. If the extent of reaction is restricted by the limiting reactant
. Select "extent of reaction" to set the extent of reaction and heat removal rate with sliders to change the outlet temperature. Select "outlet temperature" to change the outlet temperature and heat removal rate to determine the conversion, and the heat removed is fixed to the value that results in the selected outlet temperature. If the extent of reaction is restricted by the limiting reactant  , the process indicates that the limiting conversion is reached by displaying the message "limiting reactant depleted". If the outlet temperature is below 0 °C or above 1,000 °C, the message "operating conditions unrealistic" appears.
, the process indicates that the limiting conversion is reached by displaying the message "limiting reactant depleted". If the outlet temperature is below 0 °C or above 1,000 °C, the message "operating conditions unrealistic" appears.
Contributed by: Michael Wrobel and Rachael L. Baumann (November 2014)
Additional contributions by: Garret D. Nicodemus, John L. Falconer, and Nick Bongiardina
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
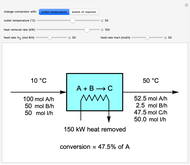
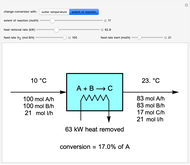
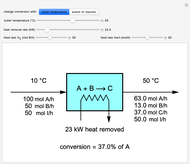
Snapshots
Details
The reaction  takes place in a reactor with heat exchange. Reactants
takes place in a reactor with heat exchange. Reactants  and
and  and inert
and inert  enter the reactor. The molar flow rates of each component exiting the reactor are calculated using the extent of reaction:
enter the reactor. The molar flow rates of each component exiting the reactor are calculated using the extent of reaction:
 ,
,
where  and
and  are the molar flow rates (mol/h) of component
are the molar flow rates (mol/h) of component  exiting and entering the reactor,
exiting and entering the reactor,  is the stoichiometric coefficient, which is positive for products and negative for reactants, and
is the stoichiometric coefficient, which is positive for products and negative for reactants, and  is the extent of reaction (mol/h).
is the extent of reaction (mol/h).
The extent of reaction is:
 ,
,
where  is the heat of formation (kJ/mol) of component i with a reference state at
is the heat of formation (kJ/mol) of component i with a reference state at  ,
,  is the constant heat capacity (kJ/[mol °C])of component i,
is the constant heat capacity (kJ/[mol °C])of component i,  is the feed temperature (°C),
is the feed temperature (°C),  is the outlet temperature (°C) and
is the outlet temperature (°C) and  is the heat added (kJ/h). The heat removed is -Q.
is the heat added (kJ/h). The heat removed is -Q.
The outlet temperature is:
 .
.
The percent conversion of A is
% conversion =  * 100.
* 100.
Note that constant heat capacities,  , were assumed for simplicity. For large temperature changes, this is not a good assumption.
, were assumed for simplicity. For large temperature changes, this is not a good assumption.
This screencast video [1] show calculations for an energy balance on a reactor with heat transfer. This screencast [2] explores limiting reagents.
References
[1] Energy Balances with Unknown Outlet Conditions [Video]. (Dec 6, 2012) www.youtube.com/watch?v=FPDPxAp-Ms0.
[2] Limiting Reagent (Interactive) [Video]. (Nov 12, 2014) www.youtube.com/watch?v=7H2EnOzGxD0&feature=youtu.be&list=PLD4476BAFA5A65111.
Permanent Citation