Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Eigenvalue Unfolding in Spacing Distributions of Random Matrices

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

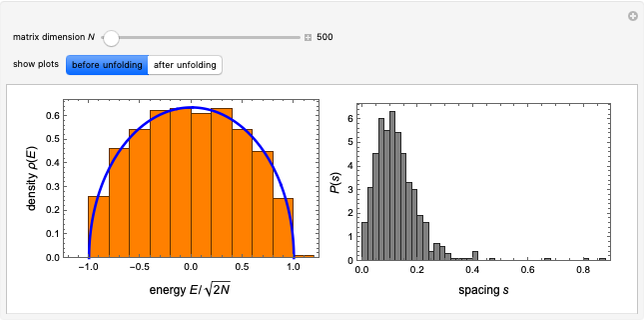
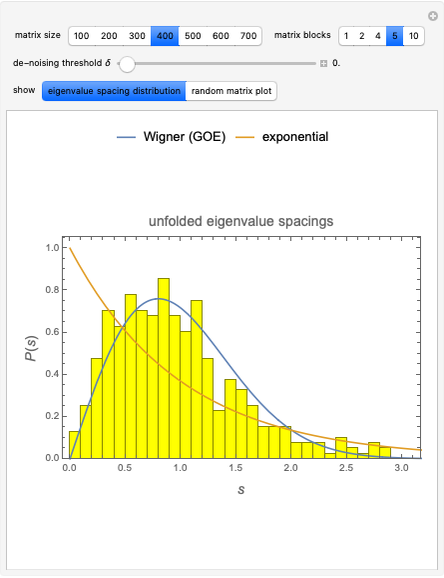
This Demonstration shows the effects of the unfolding procedure adopted in random matrix theory for rescaling eigenvalues of random Hermitian matrices before computing the nearest-neighbor spacing distribution of the matrix eigenvalues [1]. The purpose of unfolding is to separate large-scale variations in the eigenvalue spacings from local fluctuations. This can be achieved only if the local average varies on scales larger than the single-spacing scale. To achieve this goal, the average staircase function needs to be computed for the average density of eigenvalues . Then this staircase function is evaluated at each of the corresponding eigenvalues, hence . 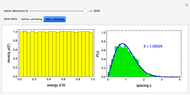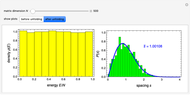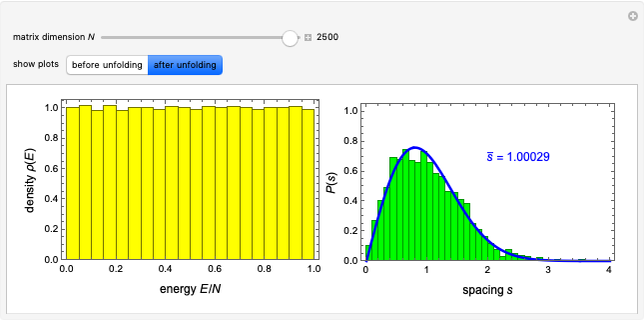The obtained sequence of unfolded eigenvalues exhibits average spacing equal to one and uniform density distribution. It is therefore straightforward to verify that the nearest-neighbor spacing distribution follows the Wigner surmise function for the Gaussian orthogonal ensemble (GOE) distribution.

[more]

Histograms for the density (left) and spacing (right) distributions show the complete set of eigenvalues from a Hermitian matrix of a chosen dimension representing the GOE distribution. Before unfolding, the (scaled) density is not uniform and is distributed according to the Wigner semicircle law (orange histogram). The spacing distribution still needs appropriate rescaling as shown in the gray histogram. After unfolding (click the setter), the normalized density is uniformly distributed (yellow histogram) and the average spacing is . The eigenvalues have been unfolded by mapping to the staircase function obtained from integrating the Wigner semicircle distribution [1]. Then, the spacing distribution of the unfolded eigenvalues (green histogram) fits the Wigner surmise function well (Wigner or GOE regime); it is plotted in blue.

Eigenvalue unfolding is not needed for random numbers sampled from a uniform distribution. In that case, the average spacing is already equal to one and the spacing distribution follows an exponential decay (Poisson regime). See the Related Links for more information.

[less]

Contributed by: Jessica Alfonsi  (June 2021)
(Padova, Italy)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Snapshot 1: default setting with matrix size

Snapshot 2: same as Snapshot 1 but with unfolded eigenvalues

Snapshot 3: unfolded eigenvalues for matrix size

References

[1] T. Timberlake, "Random Numbers and Random Matrices: Quantum Chaos Meets Number Theory," American Journal of Physics, 74(6), 2006 pp. 547–553. doi:10.1119/1.2198883.

[2] T. Timberlake. "Random Numbers and Random Matrices." (May 27, 2021) sites.berry.edu/ttimberlake/research/random-numbers-and-random-matrices.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send