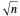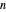Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Circular Law for Random Matrices

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

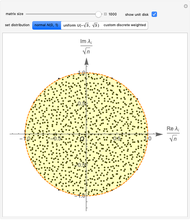
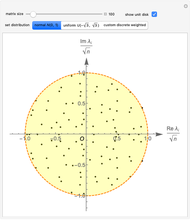
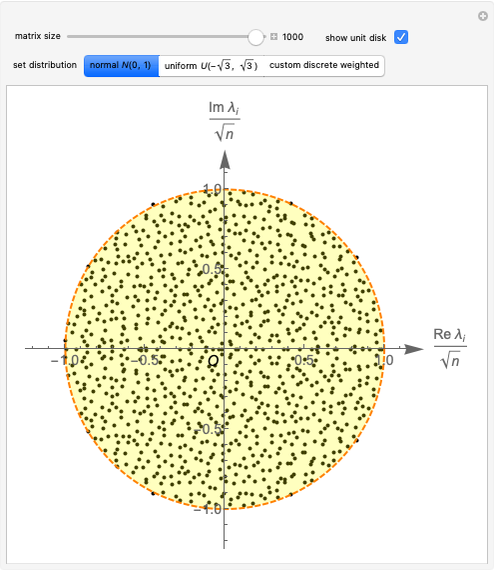
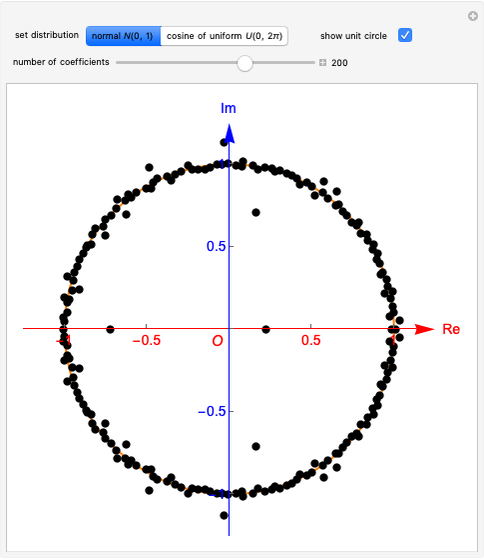
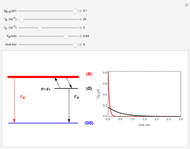
This Demonstration shows that the eigenvalues of an 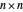random matrix with independent and identically distributed (i.i.d.) random entries, all with zero mean and unit variance, converge to the circular law in the limit as 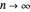. Thus the limiting spectral distribution is the uniform distribution over the unit disk in the complex plane. This behavior is universal and does not depend on the choice of the probability distribution for the law of entries (see [1] and its references).

[more]

Vary the "matrix size" to explore the convergence of the computed eigenvalues over the unit disk in the complex plane. You can set the law of the matrix entries by choosing from the normal distribution, the uniform distribution and a custom defined discrete distribution, all with mean zero and variance equal to one (for details concerning the choice of distributions see [2]). The computed eigenvalues (or the matrix entries) are scaled by a factor where is the matrix size. The checkbox control "show unit disk" can highlight the convergence over the unit complex disk.

[less]

Contributed by: Jessica Alfonsi (December 2020)
(Padova, Italy)
Open content licensed under CC BY-NC-SA

Snapshots

Details

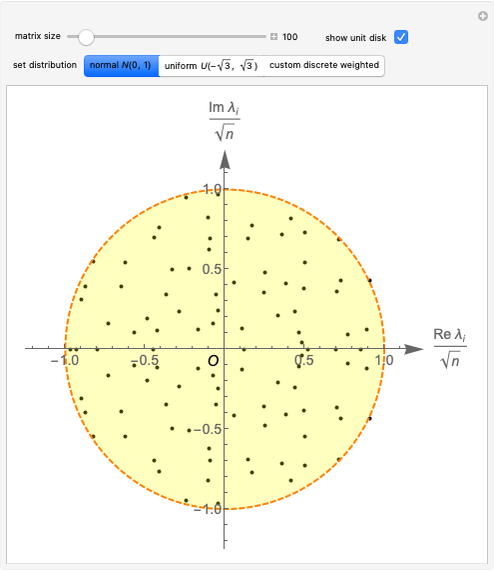
Snapshot 1: matrix entries sampled from normal distribution, 100 eigenvalues, limit disk highlighted

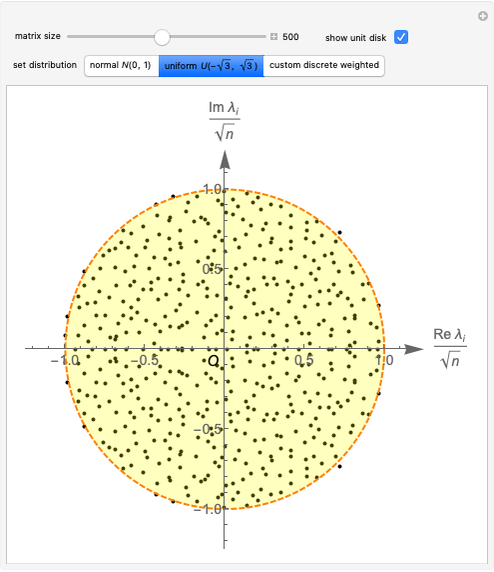
Snapshot 2: matrix entries sampled from uniform distribution, 500 eigenvalues, limit disk highlighted

Snapshot 3: matrix entries sampled from custom discrete distribution, 800 eigenvalues, limit disk not highlighted

References

[1] Wikipedia. "Circular Law." (Sep 21, 2020) en.wikipedia.org/wiki/Circular_law.

[2] R. Wicklin, The Circular Law for Eigenvalues (blog). (Sep 21, 2020) blogs.sas.com/content/iml/2020/04/27/circular-law-eigenvalues.html.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send