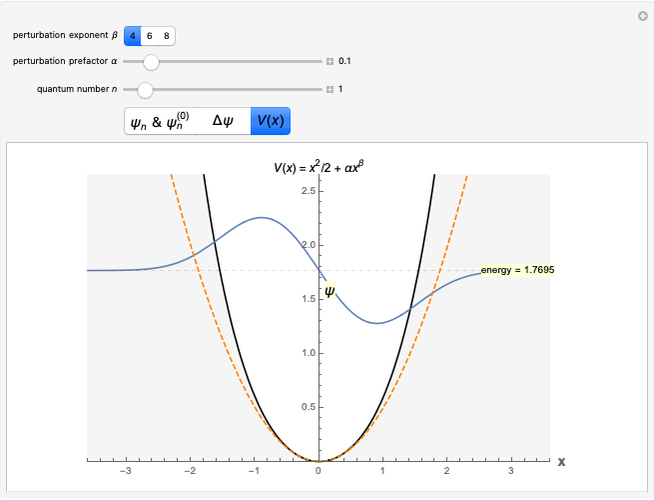
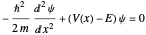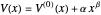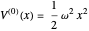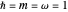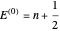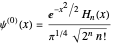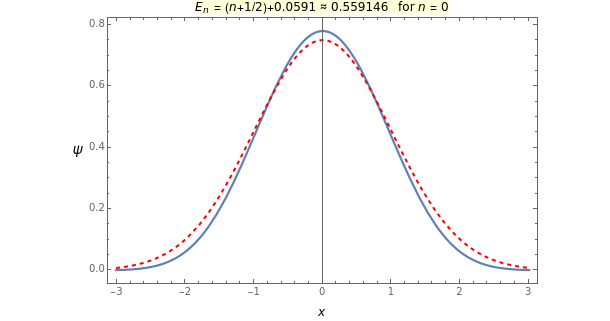
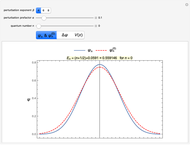
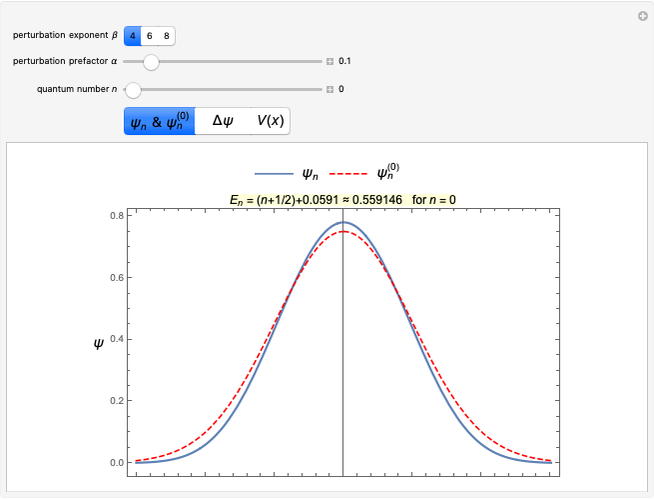
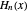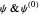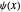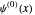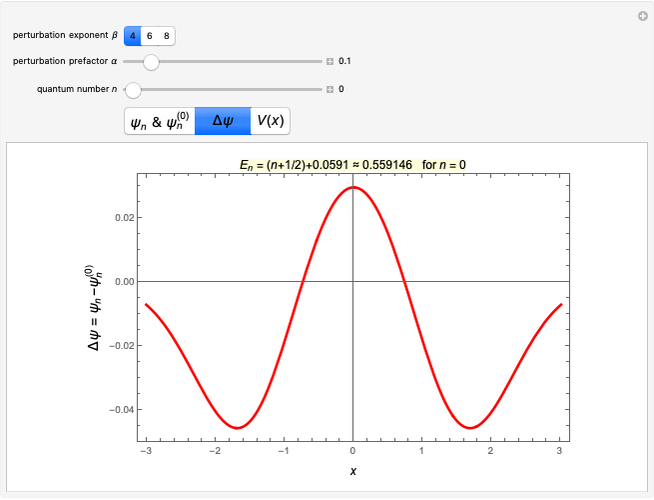
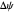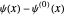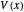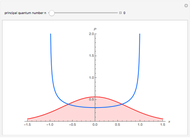
This Demonstration calculates eigenvalues and eigenfunctions for the perturbed Schrödinger equation with , where . Units are . The energies and wavefunctions for the unperturbed potential are given by and , where is a Hermite polynomial. When you select "", the numerical solution for and the unperturbed solution are plotted. When you select "", is plotted. When you select "", is shown as a solid black line, 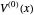as a dashed red curve and as a blue curve. The unperturbed eigenvalue is given by 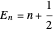in all cases.