Ellipse Rolling around a Circle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
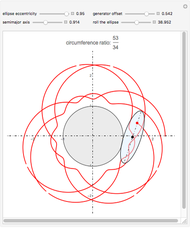
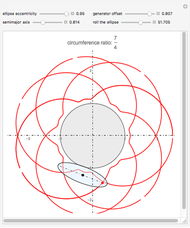
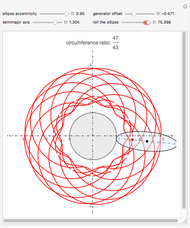
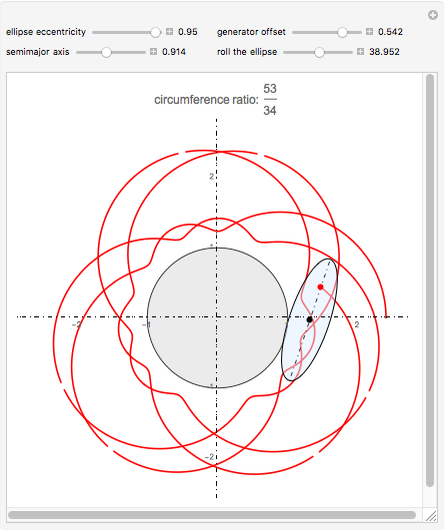
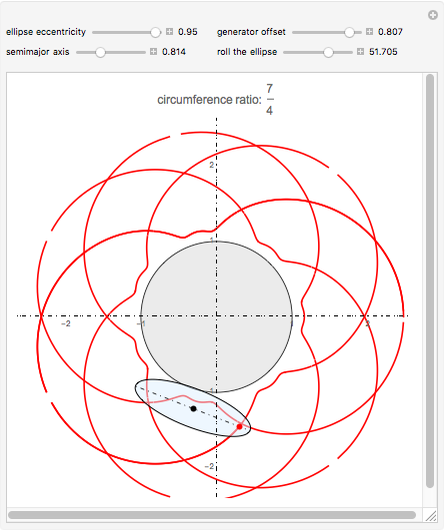
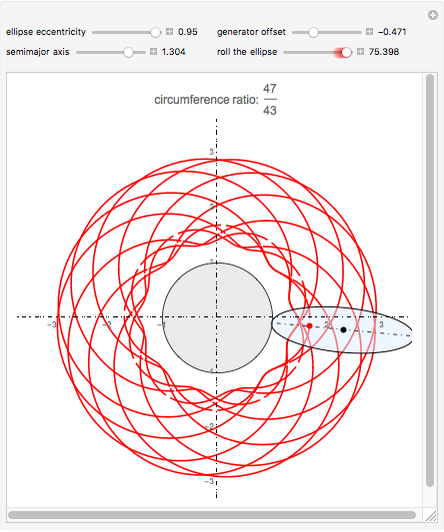
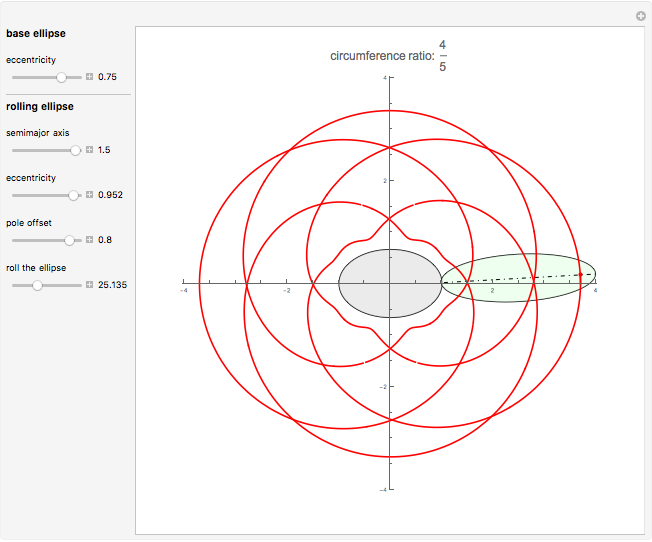
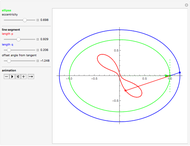
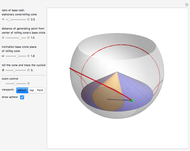
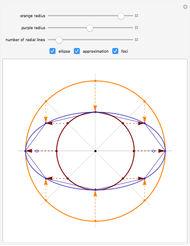
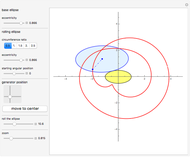
This Demonstration draws a roulette of a generator point on an ellipse that rolls without slipping around a circle.
[more]
Contributed by: Erik Mahieu (July 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
With the ellipse in its initial position to the right of the central circle, we define two points:
1. The point  on the central circle is at an arc length
on the central circle is at an arc length  from its intersection with the positive
from its intersection with the positive  axis.
axis.
2. The point  , on the ellipse in the initial position, is at an arc length
, on the ellipse in the initial position, is at an arc length  from the intersection with its semimajor axis
from the intersection with its semimajor axis
We also define two angles:
1.  is the angle subtending an arc of length
is the angle subtending an arc of length  on the circle
on the circle
2.  is the angle between the tangent line on the ellipse at
is the angle between the tangent line on the ellipse at  and the
and the  axis.
axis.
To roll the ellipse around the circle, two geometric transformations on points  on the ellipse are needed. They are performed by the function
on the ellipse are needed. They are performed by the function  :
:
1. a translation by the vector  .
.
2. a rotation around  through the angle
through the angle  .
.
Permanent Citation