Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Tangents to a Rotating Ellipse

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

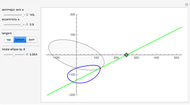
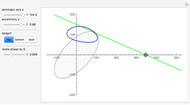
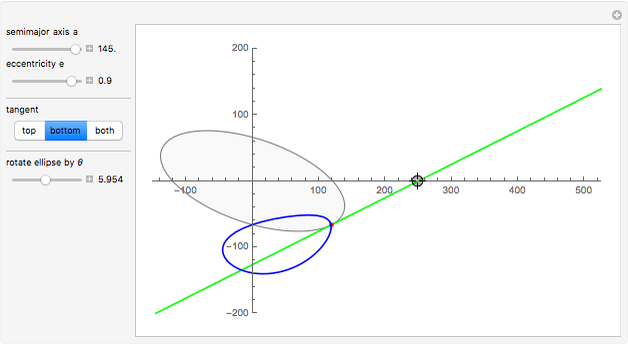
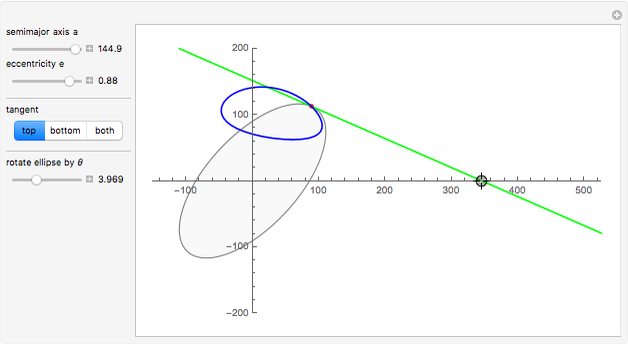
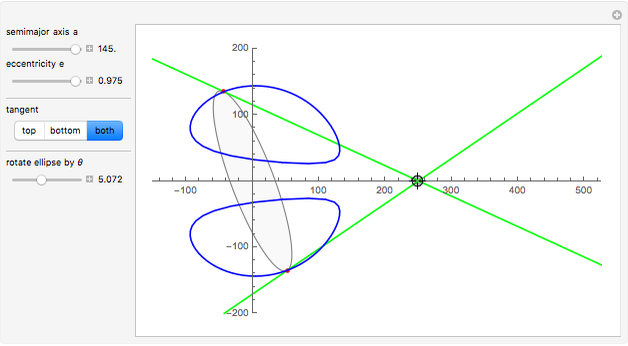
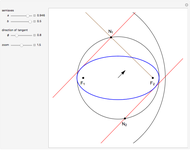
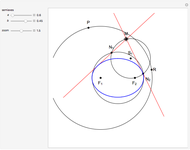
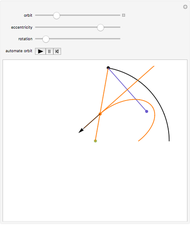
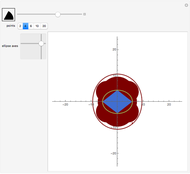
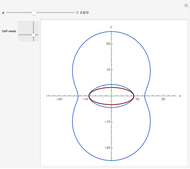
This Demonstration plots the tangents and the locus of the points of tangency to a rotating ellipse starting from a point on the axis that you can drag along the axis.

Contributed by: Erik Mahieu (November 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The equation of an ellipse with semimajor axis and eccentricity rotated by radians about its center at the origin is .

The equation of a line through the point and cutting the axis at an angle is .

Solving these two equations simultaneously gives the two points of intersection of the line with the rotating ellipse. The line is tangent if these two points coincide. This happens with the angle that satisfies the equation that sets the two coordinates of the intersection points equal, .

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send