Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Pythagorean Primitive Triples Using Primes

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

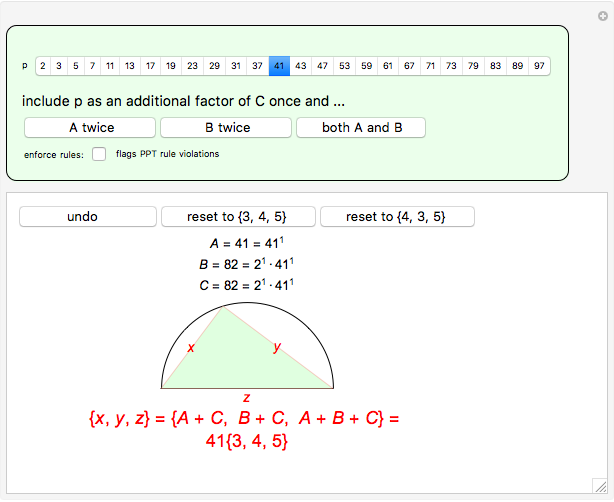
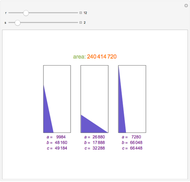
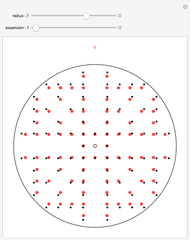
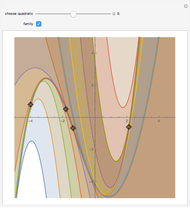
Primitive Pythagorean triangles (PPTs) are right triangles that have integer sides with no common divisor. They were used by the Babylonians for use in excavation and surveying. Methods for finding the triples that represent PPTs were valued. A novel method is shown here.

[more]

Any (and all) Pythagorean triples can be derived starting from two integers and . You can change the values of and by multiplying their current values by prime numbers. To do this, first click one of the two reset buttons and then repeat the following two steps:

1) choose a prime value from the setter bar at the top.

2) click one of the buttons labeled "A twice", "B twice", or "both A and B".

To generate PPTs, keep and relatively prime as described in the details.

[less]

Contributed by: Robert L. Brown (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

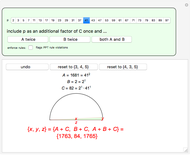
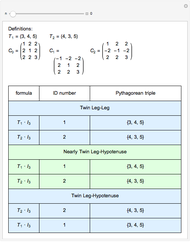
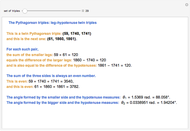
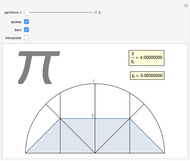
The early Greeks used Euclid's formula to calculate PPTs from two relatively prime integers and , where : .

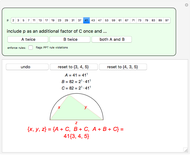
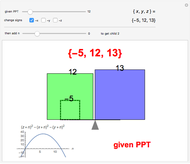
The parametrization offered here is similar and amounts to a change of variables. Let and be relatively prime and . Then is a PPT.

Not only is this parametrization very pretty, it can be generalized and has been used in the examination of Fermat's last theorem.

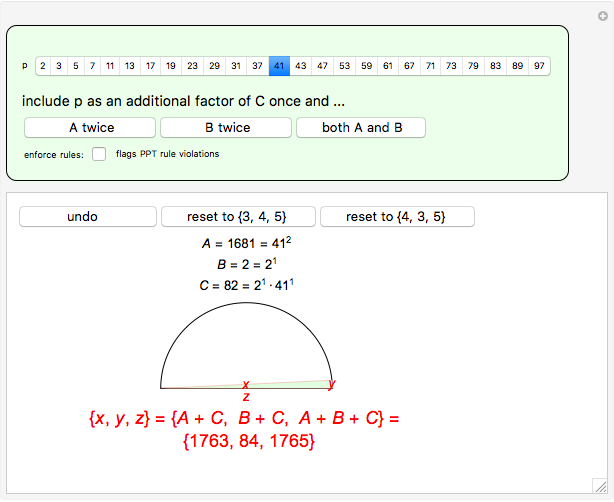
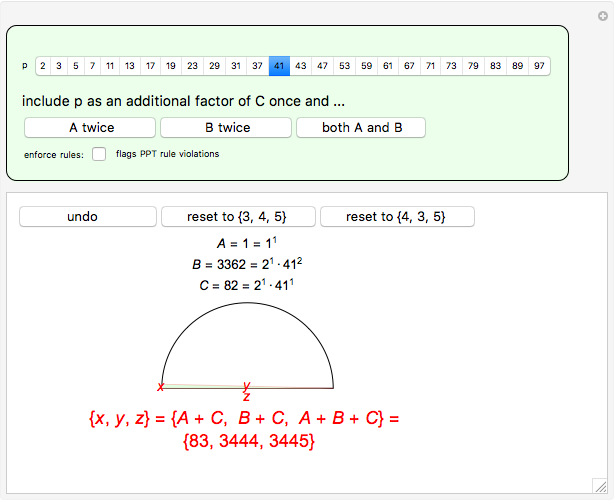
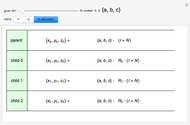
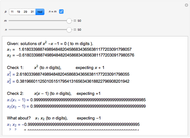
In order to generate only PPTs, and must be relatively prime.

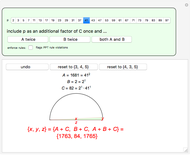
1) Never press the "both A and B" button.

2) Never include a prime as an additional factor in or if that prime is already a factor of the other integer.

Select the checkbox "enforce rules:" to be warned that the relatively prime rule is violated.

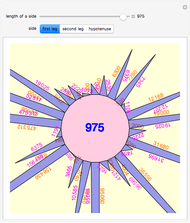
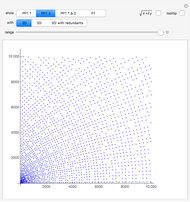
The prime factors of the resulting PPT sides can be examined by mousing over the number of interest.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send