Exploring the Times Table

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
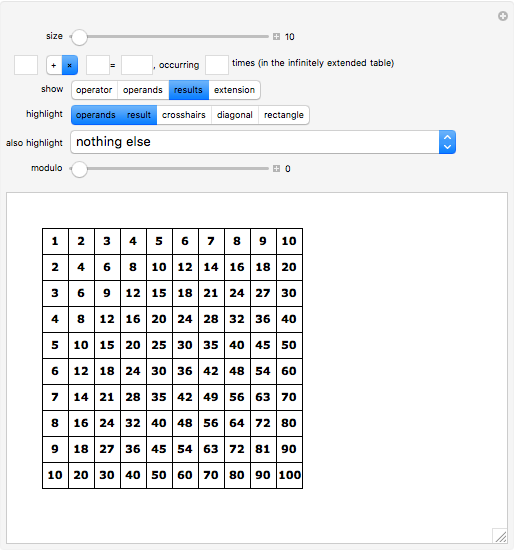
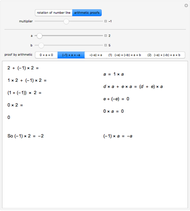
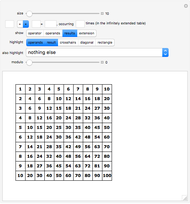
The times table provides a rich source for mathematical discoveries. The plus table, on the other hand, is pretty dull. This Demonstration lets you explore both for comparison.
[more]
Contributed by: Tom Verhoeff (March 2011)
(Eindhoven University of Technology)
Open content licensed under CC BY-NC-SA
Snapshots
Details
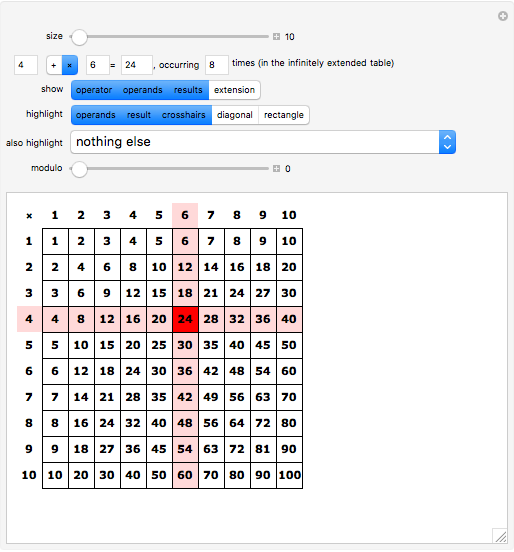
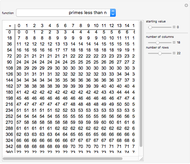
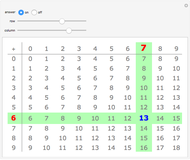
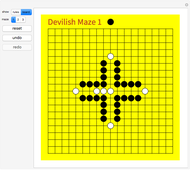
When counting occurrences in the times table, it is best to imagine it infinitely extended. This is reinforced by clicking "extension". How often does the result 1 occur? Once! And 2? Twice! And 3? Also twice! Any others that occur exactly twice? These turn out to be the prime numbers. And 4? It occurs three times. Any others occurring exactly three times? Is there a pattern to how often a number occurs?
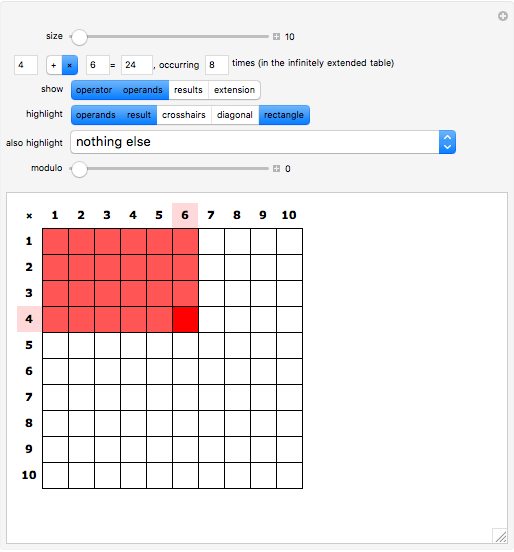
To help in this exploration, you can use the "also highlight" control. In its default setting, it only highlights the result. In its third setting, it will highlight all cells containing a value equal to the selected result, including in the right and bottom border if those occurrences fall outside the shown table range. This simplifies the counting of occurrences.
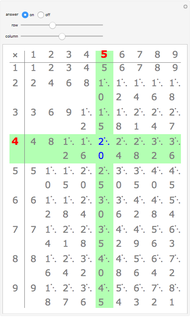
The fourth setting of the "also highlight" control highlights all cells that occur the same number of times as the selected result. Select result 6 to see all values that occur 4 times. What is special about these values?
The fifth setting highlights all cells whose occurrence count has the same parity (odd or even) as the selected result. This way, you can easily see all values that occur an odd number of times. Just select 4.
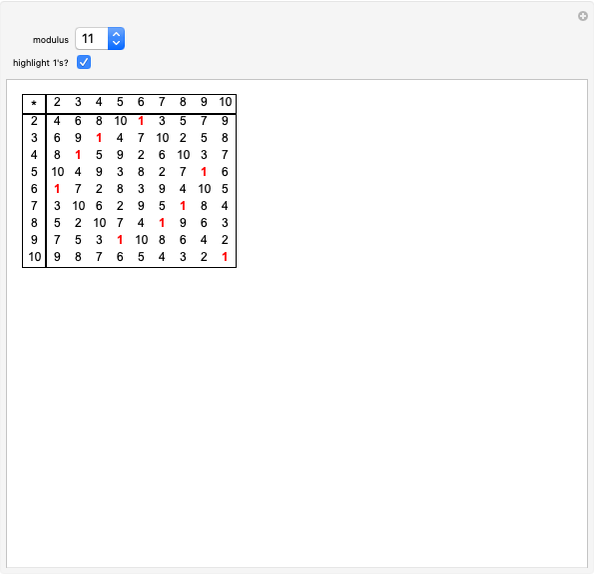
The "modulo" slider highlights cells whose value equals the selected result modulo the slider's value or whose value is divisible by the slider's value if no result is selected. This gives rise to nice patterns. Can you understand those patterns?
These explorations show that the times table is full of surprises. There are some regularities, but otherwise it is a very rich world, containing the seeds of advanced mathematics.
Permanent Citation
"Exploring the Times Table"
http://demonstrations.wolfram.com/ExploringTheTimesTable/
Wolfram Demonstrations Project
Published: March 7 2011