Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Finding Strange Attractors of Iterated Maps

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

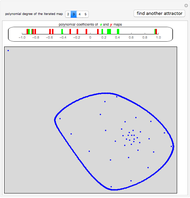
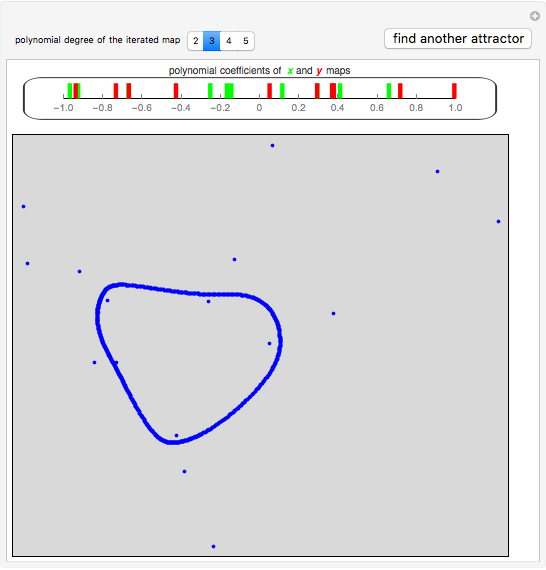
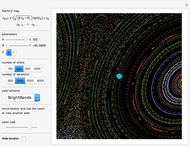
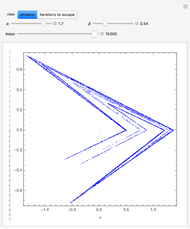
This Demonstration searches for strange attractors of a nonlinear two-dimensional polynomial map. Both the and the polynomial maps of degree are defined by coefficients , one for each term , , .

[more]

To find an attractor, we compare two orbits of the map with the same coefficients but starting from nearby initial points. If the orbits become unbounded or move apart, another set of random coefficients is selected. If successive iterations move the orbits increasingly closer together, an attractor is detected and plotted and the search is stopped.

[less]

Contributed by: Erik Mahieu (April 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The strange attractors from the map used in this Demonstration and many others are described extensively in [1].

Reference

[1] J. C. Sprott, Strange Attractors: Creating Patterns in Chaos, New York: M&T Books, 1993.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send