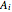Folding a Strip to Converge to an Equilateral Triangle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
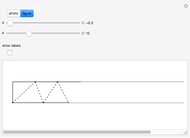
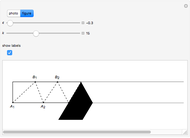
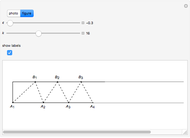
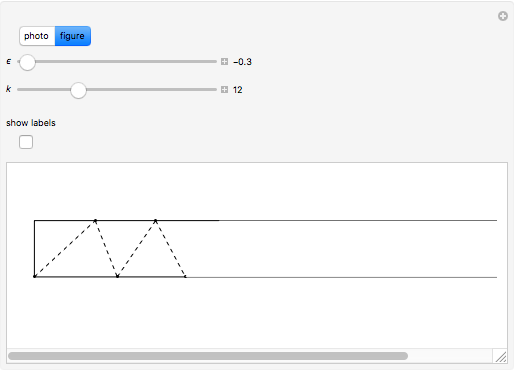
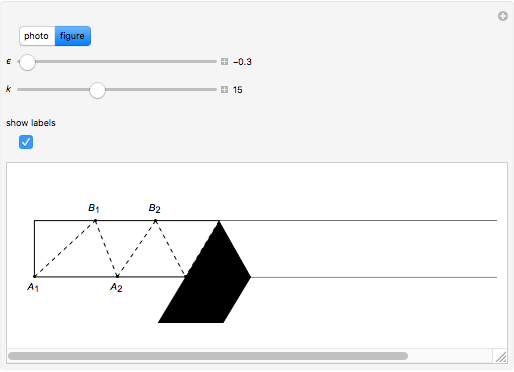
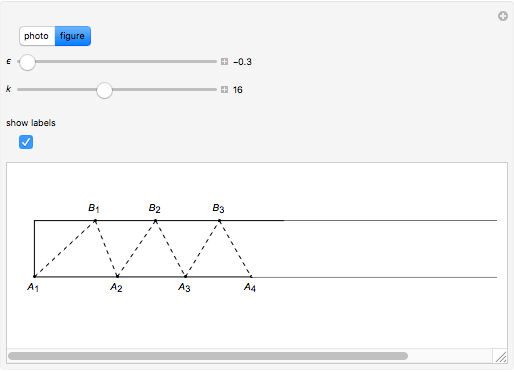
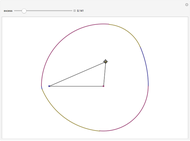
Begin with a long strip of gummed tape. Fold it up in any way you like, then unfold it, fold it down, and repeat as in the photo. The number of steps can be selected with the  slider.
slider.
Contributed by: Izidor Hafner (February 2016)
Open content licensed under CC BY-NC-SA
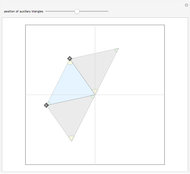
Snapshots
Details
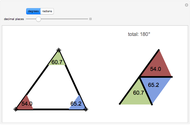
Folding down means bisecting the angle 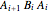 . If the initial angle at
. If the initial angle at 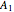 is
is 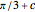 , then the angle at
, then the angle at  is
is  , which rapidly approaches
, which rapidly approaches 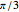 as
as  . Since that is the angle at the top of an isosceles triangle, the other two angles approach
. Since that is the angle at the top of an isosceles triangle, the other two angles approach 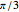 as well. The same argument is valid for the triangles
as well. The same argument is valid for the triangles  [1, pp. 11–12, 57].
[1, pp. 11–12, 57].
Reference
[1] P. Hilton and J. Pedersen, Build Your Own Polyhedra, Menlo Park, CA: Addison-Wesley, 1994.
Permanent Citation