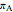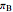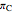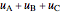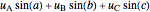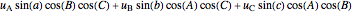Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Four Theorems on Spherical Triangles

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

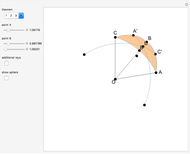
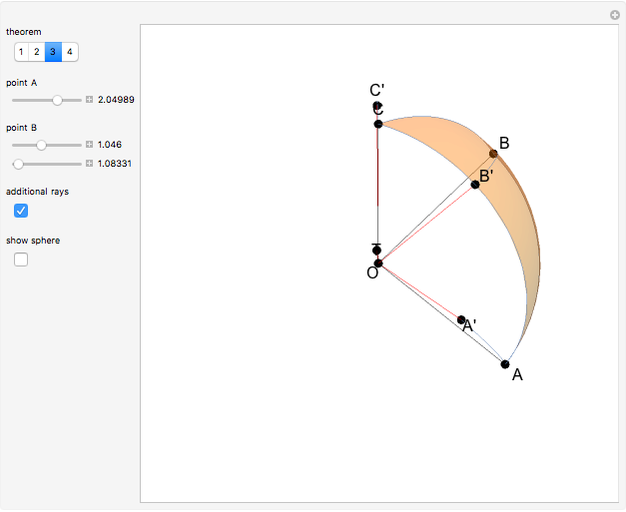
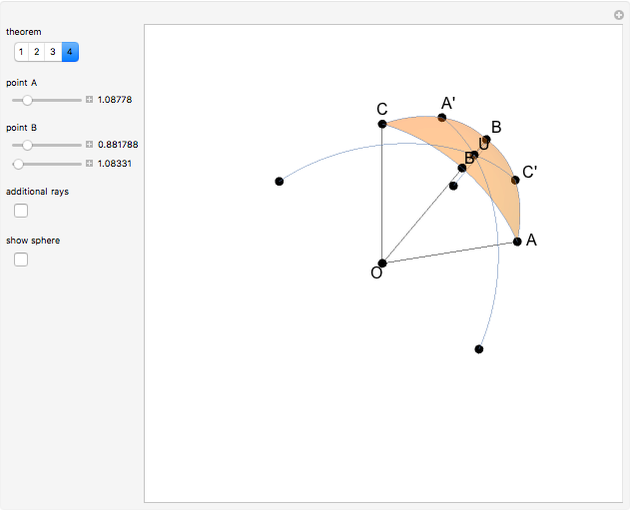
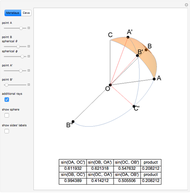
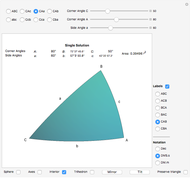
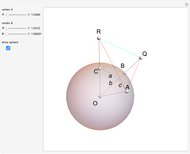
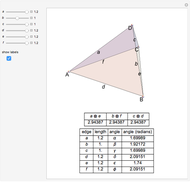
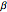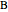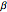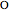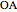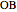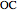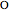Draw a spherical triangle on the surface of a unit sphere centered at . Let the sides opposite the corresponding vertices be the arcs , , . Let , , be the angles at the vertices , , ; , , are also the dihedral angles of a trihedron with apex and edges , , . Let , , be the angles of at . Let 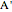, , 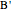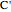be points on the sides (or their extensions) opposite to , , 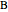. Define the unit vectors , , .

[more]

This Demonstration illustrates the following four theorems:

1. Let be the plane through and the bisector of the arc opposite ; define and similarly. Then , , meet along a common straight line , which is parallel to .

2. The bisector planes of the dihedral angles , , of the trihedron meet along a common straight line , which is parallel to .

3. The planes through the edges , , and orthogonal to the opposite faces of meet along a common straight line , which is parallel to .

4. The planes through the perpendicular bisectors of the faces of meet along a common straight line , which is parallel to .

[less]

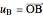Contributed by: Izidor Hafner (March 2017)
Open content licensed under CC BY-NC-SA

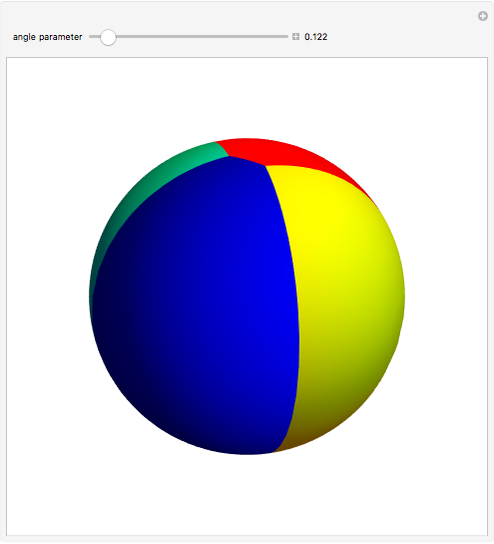
Snapshots

Details

This Demonstration is based on problem 5.34 in [3, p. 88].

References

[1] Wikipedia. "Spherical Law of Cosines." (Mar 15, 17) en.wikipedia.org/wiki/Spherical_law_of _cosines.

[2] Wikipedia. "Spherical Trigonometry." (Mar 15, 2017) en.wikipedia.org/wiki/Spherical_trigonometry.

[3] V. V. Prasolov and I. F. Sharygin, Problems in Stereometry (in Russian), Moscow: Nauka, 1989.

[4] Wikipedia. "Ceva's Theorem." (Mar 15, 2017) en.wikipedia.org/wiki/Ceva%27 s_theorem.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send