Fourier Series Approximation to Equilateral Triangle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
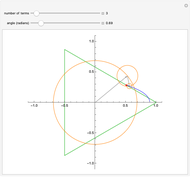
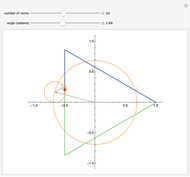
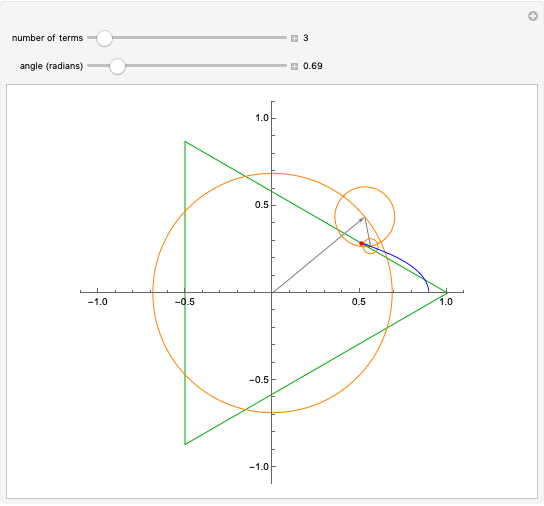
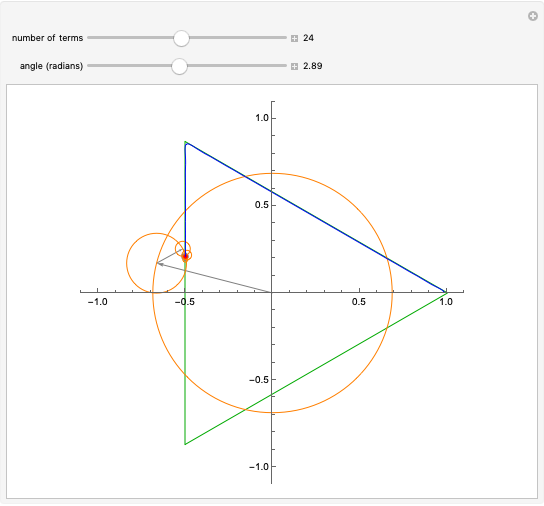
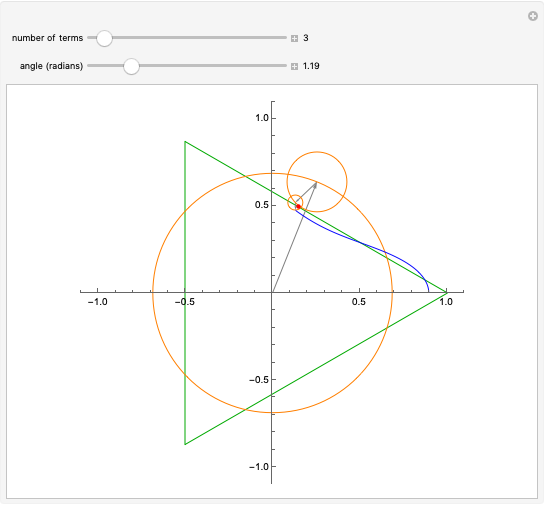
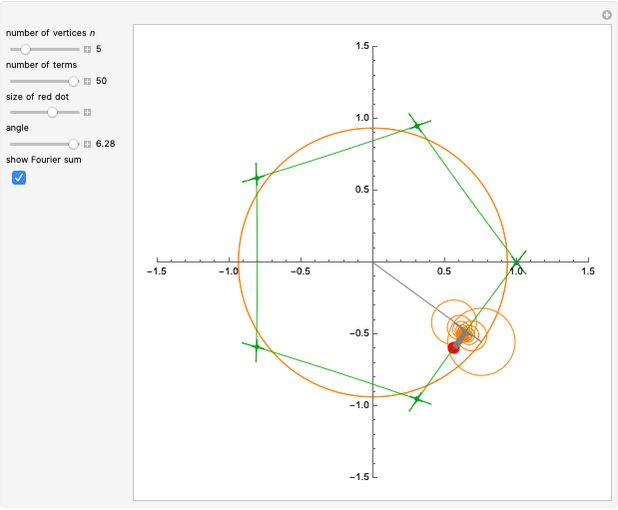
This Demonstration shows Fourier series approximations to the function tracing an equilateral triangle, shown in green, in the complex plane. The vector representing each additional term (gray) is shown, along with its encompassing circle (orange). The blue curve represents a partial sum of the Fourier series, with the selected number of terms. The red dot shows the parametrization of the triangle.
Contributed by: Walden Freedman (August 2022)
After work by: Grant Sanderson (3Blue1Brown)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Let  be the piecewise-continuous function giving a parametrization of the equilateral triangle in the complex plane:
be the piecewise-continuous function giving a parametrization of the equilateral triangle in the complex plane:
The function 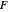 is defined in the initialization code using the function UnitStep. The Fourier series is then given by
is defined in the initialization code using the function UnitStep. The Fourier series is then given by 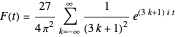 .
.
The function 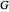 defined in the initialization code produces the sequence
defined in the initialization code produces the sequence 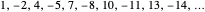 ; the function
; the function 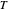 then sums the terms of the Fourier series in the same order.
then sums the terms of the Fourier series in the same order.
The slider marked "angle" controls the angle between the gray vector from the origin and the positive  axis between
axis between  and
and 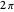 . The slider marked "number of terms" controls the number of terms in the partial sum, which equals the number of orange circles and gray vectors, from 1 to 50. The accuracy of the approximations, in the sense of the norm, improves as
. The slider marked "number of terms" controls the number of terms in the partial sum, which equals the number of orange circles and gray vectors, from 1 to 50. The accuracy of the approximations, in the sense of the norm, improves as 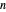 increases. But interestingly, the graph "wobbles" more when
increases. But interestingly, the graph "wobbles" more when 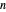 is odd. This is presumably because in that case the last term (which rotates in the positive direction) has no term with opposite rotation to compensate. The blue curve is the Fourier approximation, while the red dot shows the parametrization of the triangle.
is odd. This is presumably because in that case the last term (which rotates in the positive direction) has no term with opposite rotation to compensate. The blue curve is the Fourier approximation, while the red dot shows the parametrization of the triangle.
This Demonstration is inspired by the videos on Fourier Series by Grant Sanderson of 3Blue1Brown. There are other related animations online, such as https://isaacvr.github.io/coding/fourier_transform.
References
[1] E. M. Stein and R. Shakarchi, Fourier Analysis: An Introduction, Princeton, NJ: Princeton University Press, 2003.
[2] F. A. Farris, Creating Symmetry: The Artful Mathematics of Wallpaper Patterns, Princeton, NJ: Princeton University Press, 2015.
Permanent Citation