Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Numerical Approximation of the Fourier Transform by the Fast Fourier Transform (FFT) Algorithm

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

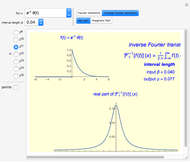
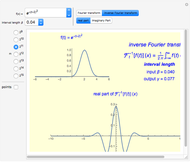
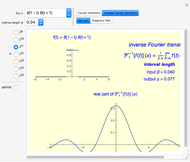
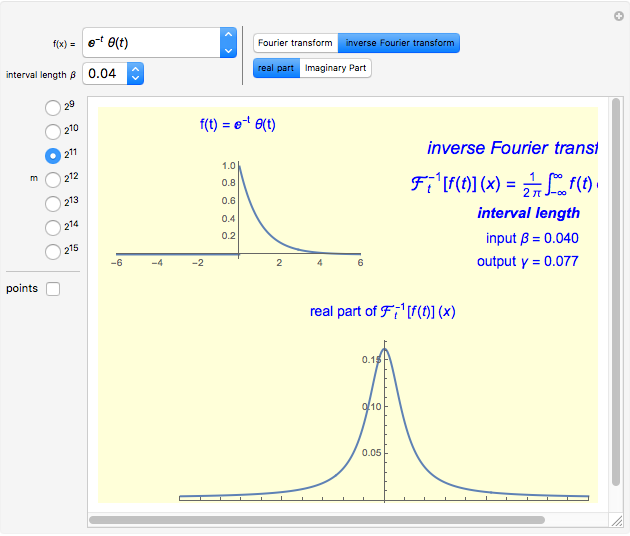
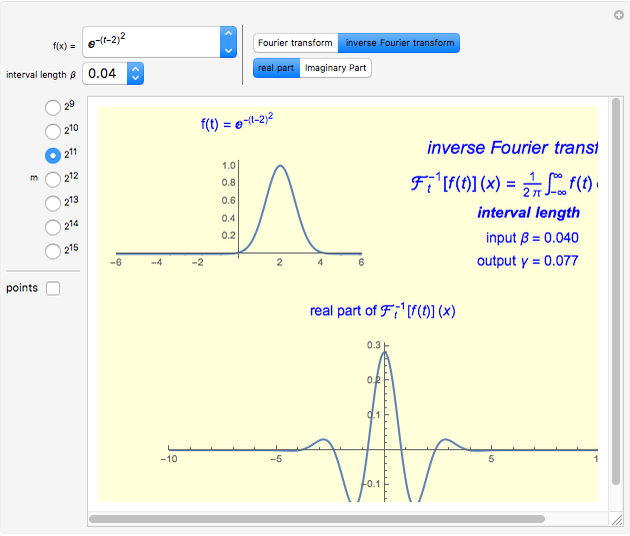
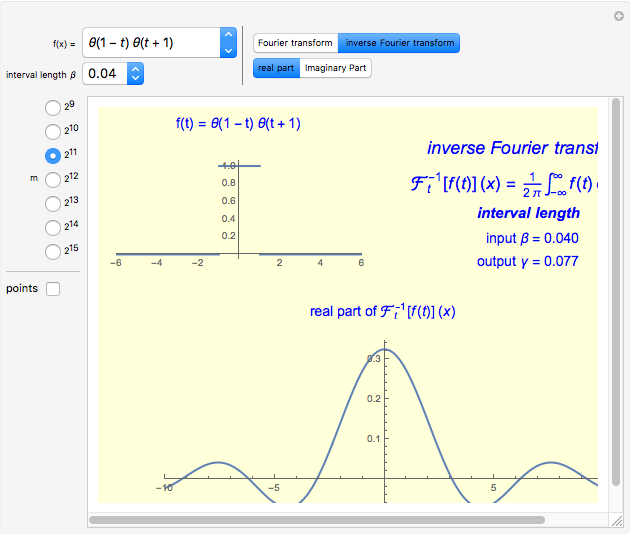
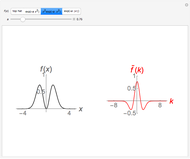
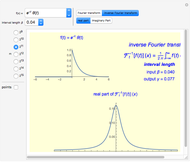
The Fourier transforms of some classical functions are calculated and their real and imaginary parts are plotted. The Fourier transform (FT) is numerically calculated by using the step function approximation to the Fourier integral; this finally leads to the discrete Fourier transform (DFT).

[more]

The DFT is rapidly evaluated by using the fast Fourier transform (FFT) algorithm. The list of data for the FFT is obtained from a finite number of sample points using an initial function. The number of sample points is chosen to be an integer power of 2, which is convenient for the evaluation of the FFT. To obtain accurate results for the continuous Fourier transform (CFT) the sample spacing must be small enough and the number of sample points must be large. This implies that the list of values at sample points for a given initial function contains many zeros, because the sampling range becomes very wide. After evaluating the FFT, the output list also contains a large number of zeros, but only the central fraction of the output list is of interest. The final result of this procedure is the continuous Fourier transform in the form of points whose spacing depends on the number of the input sample points and its sample spacing. These facts make the straightforward application of the FFT to the numerical approximation of the Fourier transform fundamentally inflexible.

Usually this procedure is used when the input sample spacing and output spacing are comparable. This Demonstration lets you control this aspect of the algorithm. The accuracy of the continuous Fourier transform is visible when the values of data points number and the sample spacing are changed.

The method is fast and reliable for functions that tend to zero quickly for large absolute values of the argument. This condition on the function is needed to avoid an undesirable aliasing effect. The algorithm is very useful in performing a fast continuous Fourier transform for numerical data.

[less]

Contributed by: Blazej Radzimirski (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The continuous Fourier transform (CFT) of a function 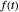and its inverse are defined by

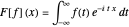
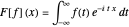InlineMathColumns=,Columns

InlineMathColumns=.Columns

A numerical approximation of the CFT requires evaluating a large number of integrals, each with a different integrand, since the values of this integral for a large range of are needed.

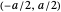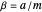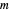The FFT can be effectively applied to this problem as follows. Let us assume that is zero outside the interval . Let be the sample spacing in for the input values of 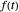, which are assumed to be centered at zero, where 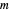is even. The values of 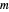and 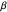are chosen at the beginning in this procedure so the range of the interval 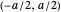is changing and depends on these parameters. The abscissas for the input data are , 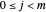. Then we can write

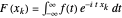
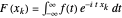InlineMathColumns

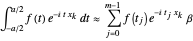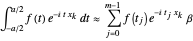=InlineMathColumns=Columns

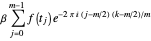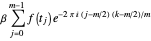=InlineMathColumns=Columns

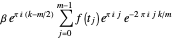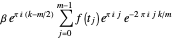=InlineMathColumns=Columns

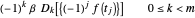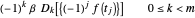=InlineMathColumns=.Columns

We define , 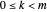. This is necessary for the above expression to be in the form of the DFT, denoted here by :

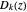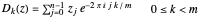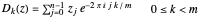..InlineMathColumns

The sample spacing (i.e., the resolution) of the result is fixed at the value 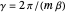as soon as one specifies the number 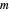of sample points and their interval 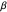. The above definition of the DFT is equivalent to the Mathematica command Fourier[list, FourierParameters->{1,-1}].

Usually, comparable sample spacing intervals in and 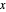are required. Then, one must put 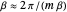, or 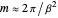. It is clear that if one wishes to obtain accurate, high-resolution results using this procedure, then it may be necessary to set very large.

More details can be found in D. H. Bailey and P. N. Swarztrauber, "A Fast Method for the Numerical Evaluation of Continuous Fourier and Laplace Transform," SIAM Journal on Scientific Computing, 15(5), 1994 pp. 1105–1110.

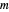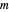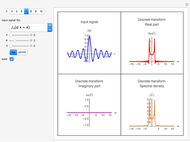
You can choose the number of data points (an integer power of two) from the radio button menu. The appropriate value of the output sample interval for a given is displayed after choosing the input sample spacing 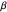. To show the sample points in the initial function (every fourth sample point is showed) and that the CFT in this algorithm is obtained in the form of points, check "points".

It is very convincing to fix a sample spacing 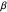from the popup menu and decrease the number of sampling points 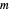: you can then observe the deterioration of the accuracy of the Fourier transform.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send