XFT: An Improved Fast Fourier Transform
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
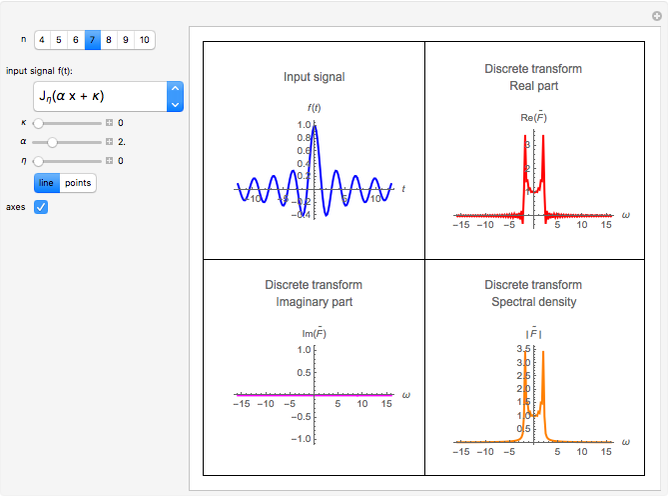
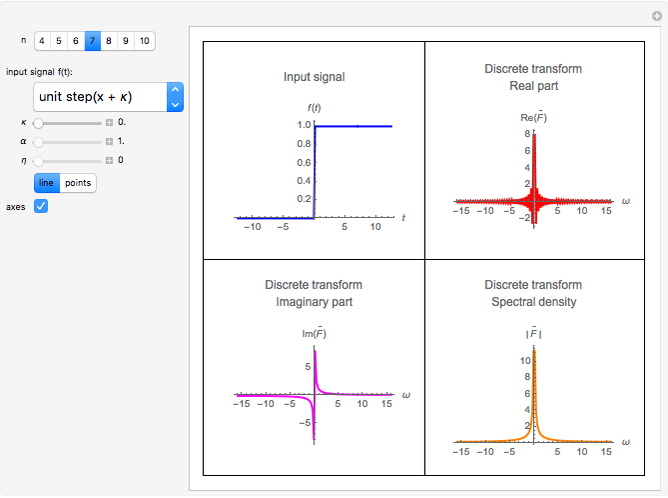
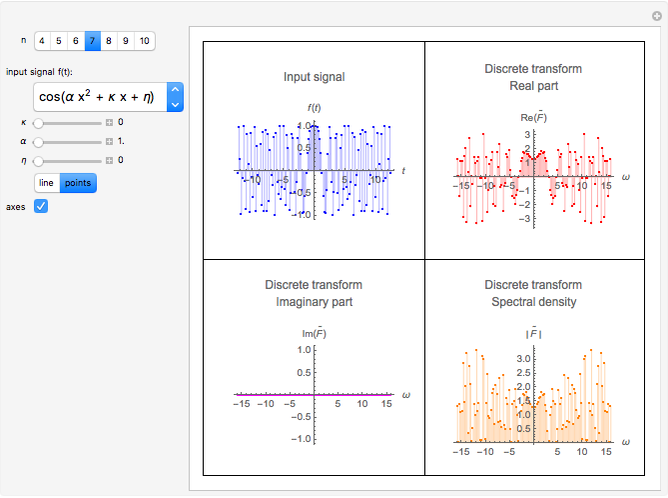
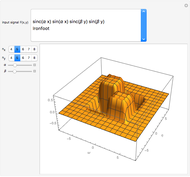
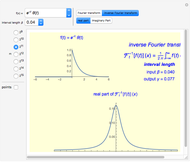
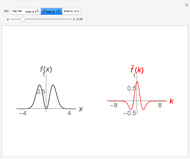
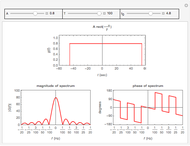
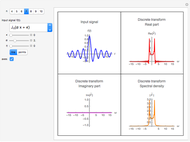
This Demonstration computes an improved fast Fourier transform that we call XFT to distinguish it from the usual FFT algorithms. The XFT is given by the product 
, where 
is a diagonal matrix with 
diagonal element given by 
, 
, 
is the standard discrete Fourier transform, and 
. Therefore, the XFT is as fast as the FFT algorithm used to compute the discrete Fourier transform. However, the output of the XFT is more accurate than the output of the FFT because it comes from an algorithm to compute the fast fractional Fourier transform based on a convergent quadrature formula. This Demonstration approximates the special case of the continuous Fourier transform defined as 
evaluated at the points 
, 
.
Contributed by: Rafael G. Campos, J. Jesus Rico Melgoza, and Edgar Chavez (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A discrete fractional Fourier transform was obtained in closed form in [1] by using finite-dimensional vectors representing Hermite functions and some asymptotic properties of the Hermite polynomials. The quadrature formula for the fractional Fourier transform obtained in [1] can be written in matrix form yielding a discrete representation of the kernel of this transform. Since this discrete fractional Fourier transform (XFT) can be written in terms of the standard discrete Fourier transform through a diagonal congruence transformation (a chirp-FFT-chirp transformation), an efficient algorithm of 
complexity for fast computations of the fractional Fourier transform can be given. This Demonstration considers the continuous Fourier transform, defined as 
.
[1] R. G. Campos, J. Rico–Melgoza, and E. Chavez, "XFT: Extending the Digital Application of the Fourier Transform," arXiv, 2009.
[2] R. G. Campos, J. Rico–Melgoza, and E. Chavez, "RFT: A Fast Discrete Fractional Fourier Transform," submitted.
Permanent Citation
XFT2D: A 2D Fast Fourier Transform
Rafael G. Campos, J. Jesus Rico Melgoza, and Edgar Chavez
Numerical Approximation of the Fourier Transform by the Fast Fourier Transform (FFT) Algorithm
Blazej Radzimirski
Fourier Transform Pairs
Porscha McRobbie and Eitan Geva
Rectangular Pulse and Its Fourier Transform
Nasser M. Abbasi
Fourier Series of Simple Functions
Alain Goriely
Amplitude and Phase in 2D Fourier Transforms
Katherine Rosenfeld
Fractional Fourier Transform
Enrique Zeleny
From Continuous- to Discrete-Time Fourier Transform by Sampling Method
Nasser M. Abbasi
Discrete Fourier Sine and Cosine Transforms
Daniel de Souza Carvalho
Pulse Fourier Approximation
Eric Mockensturm
